以下茎叶图记录了甲,乙两组各四名同学的植树棵树,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(1)如果X=8,求乙组同学植树棵树的平均数和方差;
(2)如果X=9,分别从甲,乙两组中随机选取一名同学,求这两名同学的植树总棵树为19的概率.
已知各项均为正数的数列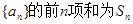 ,
,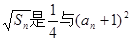 的等比中项。
的等比中项。
(1)求证:数列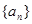 是等差数列;
是等差数列;
(2)若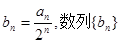 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
(12分)已知
(Ⅰ)求函数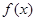 图象的对称中心的横坐标;
图象的对称中心的横坐标;
(Ⅱ)若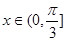 ,求函数
,求函数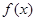 的值域。
的值域。
. 函数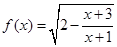 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B.
的定义域为集合B.
(1)求A;(2)若B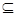 A,求实数
A,求实数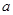 的取值范围。
的取值范围。
已知定义在(-∞,—1)∪(1,+∞)上的奇函数满足:①f(3)=1;②对任意的x>2, 均有f(x)>0,③对任意的x>0,y>0.均有f(x+1)+f(y+1)=f(xy+1)
⑴试求f(2)的值;
⑵证明f(x)在(1,+∞)上单调递增;
⑶是否存在实数a,使得f(cos2θ+asinθ)<3对任意的θ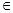 (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)求f(x)的最小正周期和最大值;
(2)若θ为锐角,且f(θ+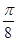 )=
)=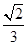 ,求tan2θ的值.
,求tan2θ的值.