为了分析某个高中学生的学习状态，对其下一阶段的学习提供指导性建议．现对他前7次考试的数学成绩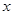
、物理成绩
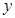进行分析．下面是该生7次考试的成绩，可见该生的物理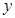成绩与数学成绩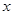是线性相关的：
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
105 |
（1）求物理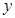成绩与数学成绩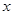的回归直线方程
；
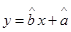（2）若该生的物理成绩达到115分，请你估计他的数学成绩大约是多少？
参考公式：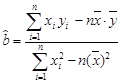
， 
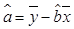
参考数据：
，
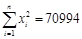
（本小题满分12分）
记函数
的定义域为集合M，函数
的定义域为集合N。求：（1）集合M，N；（2）集合M∩N，M∪N。
（本小题满分14分）
已知函数
，
，它们的定义域都是
，其中
，
（Ⅰ）当
时，求函数
的单调区间；
（Ⅱ）当时，对任意
，求证：
（Ⅲ）令
，问是否存在实数
使得
的最小值是3，如果存在，求出的值；如果不存在，说明理由。
（本小题满分14分）
一种计算装置，有一数据入口点A和一个运算出口点B ，按照某种运算程序：
①当从A口输入自然数1时，从B口得到
，记为
；
②
当从A口输入自然数
时，在B口得到的结果
是前一个结果
的
倍；
试问：当从A口分别输入自然数2 ，3 ，4 时，从B口分别得到什么数？试猜想的关系式，并证明你的结论。
（本小题满分13分）
已知函数
在
与
处都取得极值。
（Ⅰ）求函数
的解析式；
（Ⅱ）求函数在区间[-2，2]的最大值与最小值。
（本小题满分13分）
已知命题：平面上一矩形ABCD的对角线AC与边AB、AD所成的角分别为
、
（如图1），则
.用类比的方法，把它推广到空间长方体中，试写出相应的一个真命题并证明。
