设椭圆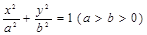 的左、右顶点分别为
的左、右顶点分别为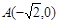 、
、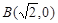 ,离心率
,离心率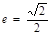 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且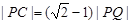 .
.
(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线MN过椭圆的右焦点与椭圆相交于M、N两点,且 ,求直线MN的方程.
,求直线MN的方程.
(本小题满分12分)设函数
(1)求函数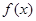 的极值点;
的极值点;
(2)当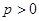 时,若对任意的
时,若对任意的 ,恒有
,恒有 ,求
,求 的取值范围;
的取值范围;
(3)证明: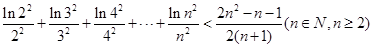
(本小题满分12分)已知二次函数 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点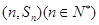 均在函数
均在函数 的图像上.
的图像上.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,
, 是数列
是数列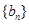 的前n项和,求使得
的前n项和,求使得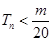 对所有
对所有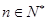 都成立的最小正整数m.
都成立的最小正整数m.
(本小题满分12分)若对任意x∈R,不等式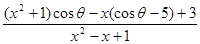 >sinθ-1恒成立,求θ的取值范围.
>sinθ-1恒成立,求θ的取值范围.
(本小题满分12分)已知 ,其中
,其中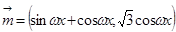 ,
, ,且
,且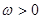 ,若
,若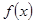 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于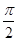 。
。
(1)求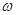 的取值范围.
的取值范围.
(2)在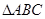 中,
中, 、
、 、
、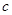 分别是角
分别是角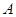 、
、 、
、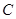 的对边,
的对边, ,
, ,当
,当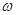 最大时,
最大时, ,求
,求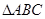 的面积.
的面积.
(本小题满分12分)设函数 的定义域为
的定义域为 ,命题
,命题 与命题
与命题 ,若
,若 真,
真, 假,求实数
假,求实数 的取值范围.
的取值范围.