已知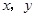 都是非零实数,且
都是非零实数,且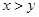 ,求证:
,求证: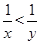 的充要条件是
的充要条件是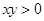 .
.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,已知AB=a,AC=2,
AA1=1,点D在棱B1C1上,且B1D∶DC1=1∶3.
(Ⅰ)证明:BD⊥A1C;
(Ⅱ)若二面角B-A1D-B1的大小为60º,试求a的值.
将3个完全相同的小球随机地放入编号依次为1,2,3,4,5的盒子里,用随机变量 表示有球盒子编号的最大值.
表示有球盒子编号的最大值.
(Ⅰ)求 ;
;
(Ⅱ)求 的分布列和数学期望
的分布列和数学期望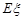 .
.
已知函数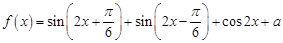 (
(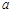 为常数)的最大值是3.
为常数)的最大值是3.
(Ⅰ)求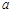 的值;
的值;
(Ⅱ)在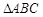 中,
中,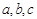 分别是角
分别是角 的对边,
的对边, ,求
,求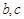 的值.
的值.
某单位为绿化环境,移栽了甲、乙两种大树各2株。设甲、乙两种大树移栽的成活率分别为
和
,且各株大树是否成活互不影响。求移栽的4株大树中:
(Ⅰ)至少有1株成活的概率;
(Ⅱ)两种大树各成活1株的概率。
(本小题满分12分)已知定义在 上的两个函数
上的两个函数 的图象在点
的图象在点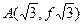 处的切线倾斜角的大小为
处的切线倾斜角的大小为 (1)求
(1)求 的解析式;(2)试求实数k的最大值,使得对任意
的解析式;(2)试求实数k的最大值,使得对任意 恒成立;(3)若
恒成立;(3)若
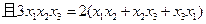 ,求证:
,求证: