某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(Ⅰ)求应从小学、中学、大学中分别抽取的学校数目;
(Ⅱ)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率.
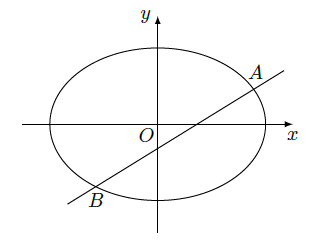
已知
,直线
,椭圆
,
分别为椭圆
的左、右焦点.
(Ⅰ)当直线
过右焦点
时,求直线
的方程;
(Ⅱ)设直线
与椭圆
交于
两点,
,
的重心分别为
.若原点
在以线段
为直径的圆内,求实数
的取值范围.
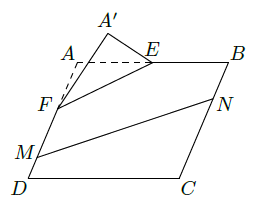
如图,在矩形 中,点 分别在线段 上, .沿直线 将 翻折成 ,使平面 .
(Ⅰ)求二面角
的余弦值;
(Ⅱ)点
分别在线段
上,若沿直线
将四边形
向上翻折,使
与
重合,求线段
的长.
如图,一个小球从 处投入,通过管道自上而下落 或 或 。已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到 , , ,则分别设为l,2,3等奖.

(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量
为获得
(
)等奖的折扣率,求随机变量
的分布列及期望
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量
为获得1等奖或2等奖的人次,求
.
在 中,角 所对的边分别为 ,已知 .
(I)求
的值;
(Ⅱ)当
时,求
及
的长.
在数列
中,
,且对任意
成等差数列,其公差为
.
(Ⅰ)若
,证明
成等比数列(
)
(Ⅱ)若对任意
,
成等比数列,其公比为
.证明:对任意
,有