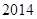 年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔
年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔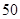 辆就抽取一辆的抽样方法抽取
辆就抽取一辆的抽样方法抽取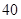 名驾驶员进行询问调查,将他们在某段高速公路的车速(
名驾驶员进行询问调查,将他们在某段高速公路的车速(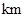 /
/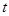 )分成六段:
)分成六段: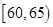 ,
,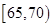 ,
,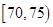 ,
, ,
, ,
,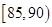 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.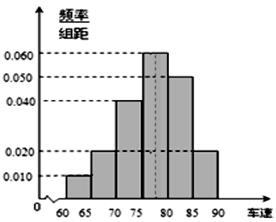
(1)求这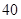 辆小型车辆车速的众数和中位数的估计值;
辆小型车辆车速的众数和中位数的估计值;
(2)若从车速在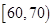 的车辆中任抽取
的车辆中任抽取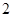 辆,求车速在
辆,求车速在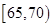 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
已知函数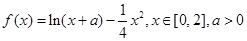 .
.
(Ⅰ)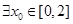 ,使得函数
,使得函数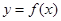 在
在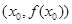 的切线斜率
的切线斜率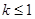 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)求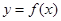 的最小值.
的最小值.
已知函数f(x)=m-|x-2|,m∈R,且f(x+2)≥0的解集为[-2,2].
(Ⅰ)求m的值;
(Ⅱ)若a,b,c∈R+,且a+b+c=m,不等式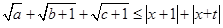 对任意实数
对任意实数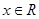 都成立,求
都成立,求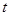 的取值范围.
的取值范围.
已知在椭圆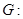
 中,
中, 分别为椭圆的左右焦点,直线
分别为椭圆的左右焦点,直线 过椭圆
过椭圆 右焦点
右焦点 ,且与椭圆的交点为
,且与椭圆的交点为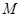 (点
(点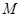 在第一象限),若
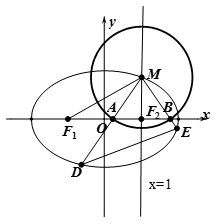
在第一象限),若 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)以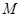 为圆心的动圆与
为圆心的动圆与 轴分别交于两点A、B,延长
轴分别交于两点A、B,延长 ,分别交椭圆
,分别交椭圆 于
于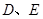 两点,判断直线
两点,判断直线 的斜率是否为定值,并说明理由.
的斜率是否为定值,并说明理由.
直四棱柱 中,底面
中,底面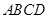 为菱形,且
为菱形,且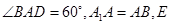 为
为 延长线上的一点,且
延长线上的一点,且 .
.
(Ⅰ) 求证: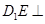 面
面 ;
;
(Ⅱ)在棱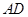 是否存在一点
是否存在一点 ,使
,使
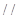 面
面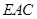 ?若存在,求
?若存在,求 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(Ⅲ)求二面角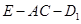 的大小;
的大小;
为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各9件样品,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图,但是乙厂记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以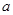 表示,规定:当产品中的此种元素含量不小于18毫克时,该产品为优等品.
表示,规定:当产品中的此种元素含量不小于18毫克时,该产品为优等品.
(Ⅰ)若甲、乙两厂产品中该种元素含量的平均值相同,求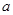 的值;
的值;
(Ⅱ)求乙厂该种元素含量的平均值超过甲厂平均值的概率;
(Ⅲ)当 时,利用简单随机抽样的方法,分别在甲、乙两厂该种元素含量超过
时,利用简单随机抽样的方法,分别在甲、乙两厂该种元素含量超过 (毫克)的数据中个抽取一个做代表,设抽取的两个数据中超过
(毫克)的数据中个抽取一个做代表,设抽取的两个数据中超过 (毫克)的个数为
(毫克)的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.