如图,平面直角坐标系 中,
中, 为坐标原点,抛物线
为坐标原点,抛物线 交x轴于A、B两点(点A在点B的左侧),交y轴于点C,以OB、OC为边作矩形OBDC,CD交抛物线于G.
交x轴于A、B两点(点A在点B的左侧),交y轴于点C,以OB、OC为边作矩形OBDC,CD交抛物线于G.
(1)求OB和OC的长;
(2)抛物线的对称轴在边OB(不包括O、B两点)上作平行移动,交x轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求PM的最大值;
(3)连接PC,在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形与△BEM相似?若存在,求出相应的m的值,并判断△PCM的形状;若不存在,请说明理由.
如图,等腰梯形ABCD中,AD∥BC,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点.
(1)求证:四边形MENF是菱形;
(2)若四边形MENF是正方形,请探索等腰梯形ABCD的高和底边BC的数量关系并证明你的结论.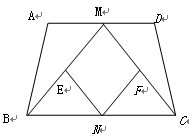
如图,一次函数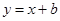 与反比例函数
与反比例函数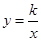 在第一象限的图象交于点B,且点B的横坐标为1,过点B作
在第一象限的图象交于点B,且点B的横坐标为1,过点B作 轴的垂线,C为垂足,若
轴的垂线,C为垂足,若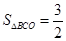 ,求一次函数和反比例函数的解析式.
,求一次函数和反比例函数的解析式.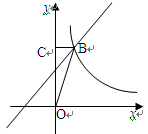
为了解某住宅区的家庭用水量情况,从该住宅区中随机抽样调查了50户家庭2010年每个月的用水量,统计得到的数据绘制了下面的两幅统计图,图1是2010年这50户家庭月总用水量的折线统计图,图2是2010年这50户家庭月总用水量的不完整的频数分布直方图.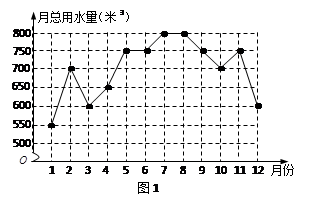
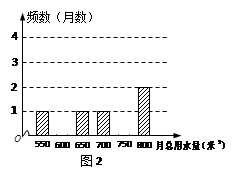
(1)根据图1提供的信息,补全图2中的频数分布直方图;
(2)在抽查的50户家庭2010年月总用水量这12个数据中,极差是米3,众数是米3,中位数是米3;
(3)请你根据上述提供的数据,计算该住宅区2010年3月份到5月份的月总用水量的平均增长率?
(结果保留1%)(参考数据: ,
, 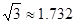 ,
,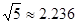 )
)
在平面直角坐标系中, ABC的三个顶点的位置如图所示,点A/的坐标是(-2,2) ,现将
ABC的三个顶点的位置如图所示,点A/的坐标是(-2,2) ,现将 ABC平移.使点A变换为点A/,点B/、C/分别是B、C的对应点.
ABC平移.使点A变换为点A/,点B/、C/分别是B、C的对应点.
(1)请画出平移后的像△A/B/C/(不写画法) ,并直接写出点B/、C/的坐标:
B/ ()、C/();
(2)若 ABC内部一点P的坐标为(a,b),则点P的对应点P/的坐标是();
ABC内部一点P的坐标为(a,b),则点P的对应点P/的坐标是();
(3) ABC的面积为:。
ABC的面积为:。
先化简,再求值: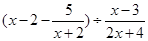 ,其中
,其中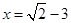 .
.