某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购
进石油 万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前
万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前 个月的需求总量
个月的需求总量 (万吨)与
(万吨)与 的函数关系为
的函数关系为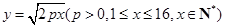 ,若区域外前4个月的需求总量为20万吨.
,若区域外前4个月的需求总量为20万吨.
(Ⅰ)试求出当第 个月的石油调出后,油库内储油量
个月的石油调出后,油库内储油量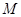 (万吨)与
(万吨)与 的函数关系式;
的函数关系式;
(Ⅱ)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定 的取值范围.
的取值范围.
(本小题满分13分)已知向量
 ,
, ,
,
定义函数 =
= 。
。
(Ⅰ)求 的最小正周期;在所给的坐标系中作出函数
的最小正周期;在所给的坐标系中作出函数 ,
, ∈
∈ 的图象
的图象
(不要求写出作图过程);
(Ⅱ)若 =2,且14≤
=2,且14≤ ≤18,求
≤18,求 的值
的值
选修4—5:不等式证明选讲
已知函数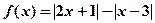 。
。
(1)解不等式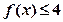 ;
;
(2)若存在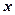 使得
使得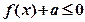 成立,求实数
成立,求实数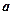 的取值范围。
的取值范围。
选修4—4:坐标系与参数方程
已知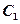 的极坐标方程为
的极坐标方程为 ,
, 分别为
分别为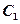 在直角坐标系中与
在直角坐标系中与 轴,
轴, 轴
轴
的交点。曲线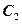 的参数方程为
的参数方程为 (
(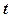 为参数,且
为参数,且 ),
), 为
为 的中点,
的中点,
(1)将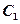 ,
,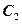 化为普通方程;
化为普通方程;
(2)求直线 (
(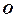 为坐标原点)被曲线
为坐标原点)被曲线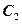 所截得弦长。
所截得弦长。
选修4-1:几何证明选讲
如图,已知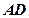 是
是 的外角
的外角 的平分线,交
的平分线,交 的延长线于点
的延长线于点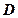 ,延长
,延长 交
交 的外接圆于点
的外接圆于点 ,连结
,连结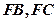 。
。
(1)求证: ;
;
(2)求证: ;
;
(3)若 是
是 外接圆的直径,
外接圆的直径,
且 ,求
,求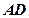 的长。
的长。
(本小题满分12分)已知函数 ,其中
,其中 为自然对数的底数,
为自然对数的底数, 。
。
(1)设 ,求函数
,求函数 的最值;
的最值;
(2)若对于任意的 ,都有
,都有 成立,
成立,
求 的取值范围。
的取值范围。