如图，已知底角为
的等腰梯形
,底边
长为7
，腰长为
，当一条垂直于底边垂足为
的直线
由
从左至右向
移动（与梯形有公共点）时，直线把梯形分成两部分，令
，记左边部分的面积为
．
（1）试求
1，3时的值；
（2）写出关于
的函数关系式．
(本题满分12分)
已知函数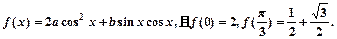
（1）求a，b的值；
（2）求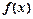
的最大值及取得最大值时x的集合；
（3）写出函数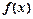在[0，
]上的单调递减区间．
（某本题满分12分）
某厂生产某种产品的年固定成本为250万元，每生产x千件，需另投入成本为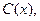
当年产量不足80千件时，
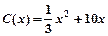（万元）；当年产量不小于80千件时，
（万元）．通过市场分析，若每件售价为500元时，该厂当年生产该产品能全部销售完．
（1）写出年利润
（万元）关于年产量x（千件）的函数解析式；
（2）年产量为多少千件时，该厂在这一产品的生产中所获利润最大，最大利润是多少？
已知函数f（x）=ax3+bx+c (a>0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导数f/(x)的 最小值为-12,求a,b,c的值．
设条件p：2x2-3x+1≤0，条件q：x2-（2a+1）x+a（a+1）≤0，若
是
的必要不充分条件，求实数a的去值范围．
（本小题14分）在平面直角坐标系中，O为坐标原点，已知向量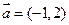
，又有点
(1)若
，且
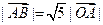，求向量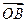
；
(2)若向量
与向量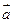
共线。当
，且函数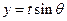
取最大值为4，求
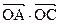的值。