如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.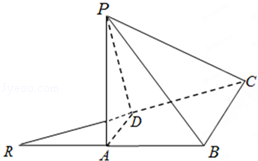
(1)求证:BC⊥PB;
(2)求二面角A﹣CD﹣P的平面角的余弦值.
已知函数 .
.
(Ⅰ)函数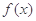 在区间
在区间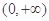 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;
(Ⅱ)当 时,
时, 恒成立,求整数
恒成立,求整数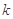 的最大值;
的最大值;
(Ⅲ)试证明: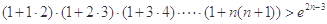 .
.
如图,已知椭圆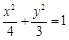 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
(Ⅰ)若点G的横坐标为 ,求直线AB的斜率;
,求直线AB的斜率;
(Ⅱ)记△GFD的面积为S1,△OED(O为原点)的面积为S2.
试问:是否存在直线AB,使得S1=S2?说明理由.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
(Ⅰ)证明:BC丄AB1;
(Ⅱ)若OC=OA,求二面角C1-BD-C的余弦值.
在某大学自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生两科的考试成绩的数据统计如图所示,其中“数学与逻辑”科目的成绩为B的考生有10人. 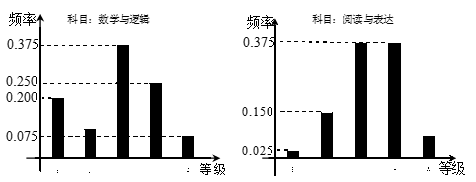
(Ⅰ)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(Ⅱ)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分.
(i)求该考场考生“数学与逻辑”科目的平均分;
(ii)若该考场共有10人得分大于7分,其中有2人10分,2人9分,6人8分. 从这10
人中随机抽取两人,求两人成绩之和的分布列和数学期望.
已知△ABC中,角A,B,C所对的边分别是a, b, c, 且2(a2+b2-c2)=3ab.
(Ⅰ)求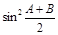 ;
;
(Ⅱ)若c=2,求△ABC面积的最大值.