如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2= (m≠0)的一个交点.
(m≠0)的一个交点.
(1)求正比例函数及反比例函数的表达式;
(2)根据图象直接回答:在第一象限内,当x取何值时,y1<y2?
解不等式组 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2﹣12x+36=0的两根,BC=4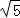 ,∠BAC=45°.
,∠BAC=45°.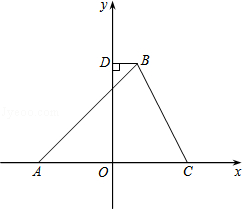
(1)求点A,C的坐标;
(2)反比例函数y= 的图象经过点B,求k的值;
的图象经过点B,求k的值;
(3)在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P,O,A为顶点的三角形相似?若存在,请写出满足条件的点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.
夏季来临,商场准备购进甲、乙两种空调.已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同.请解答下列问题:
(1)求甲、乙两种空调每台的进价;
(2)若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润y(元)与甲种空调x(台)之间的函数关系式;
(3)在(2)的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器.直接写出购买按摩器的方案.
甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
请结合图象信息解答下列问题: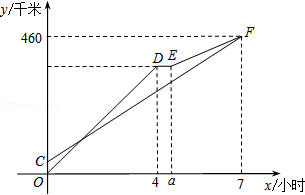
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x的函数关系式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时与甲车相距15千米?直接写出答案.