如图,过椭圆 内一点
内一点 的动直线
的动直线 与椭圆相交于M,N两点,当
与椭圆相交于M,N两点,当 平行于x轴和垂直于x轴时,
平行于x轴和垂直于x轴时, 被椭圆
被椭圆 所截得的线段长均为
所截得的线段长均为 .
.
(1)求椭圆 的方程;
的方程;
(2)在平面直角坐标系中,是否存在与点A不同的定点B,使得对任意过点 的动直线
的动直线 都满足
都满足 ?若存在,求出定点B的坐标,若不存在,请说明理由.
?若存在,求出定点B的坐标,若不存在,请说明理由.
我们从小学开始,学过的数有:零、正整数、负整数、分数、整数、无理数、实数、有理数、虚数、纯虚数、非纯虚数、复数,画出数系的结构图.
.设p:实数x满足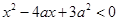 ,其中
,其中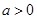 ,命题
,命题 实数
实数 满足
满足 .
.
(1)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若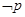 是
是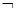
 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
已知函数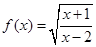 的定义域集合是A,函数
的定义域集合是A,函数 的定义域集合是B
的定义域集合是B
(1)求集合A、B
(2)若A B=B,求实数
B=B,求实数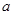 的取值范围.
的取值范围.
(12分)写出命题:“若 x+y =5,则 x = 3且 y = 2”的逆命题、否命题、逆否命题.并判断它们的真假.
如图,在棱长为1的正方体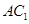 中,
中,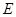 、
、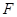 分别为
分别为 和
和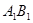 的中点.
的中点.
(1)求异面直线 和
和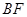 所成的角的余弦值;
所成的角的余弦值;
(2)求平面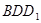 与平面
与平面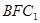 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;