已知公差不为零的等差数列{an}的前4项和为10,且a2,a3,a7成等比数列.
(1)求通项公式an;
(2)设bn=2an,求数列{bn}的前n项和Sn.
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.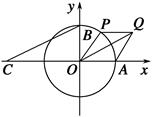
(1)求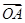 ·
·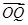 +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin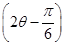 的值.
的值.
已知△ABC的内角A,B,C所对的边分别是a,b,c,设向量m=(a,b),n=(sin B,sin A),p=(b-2,a-2).
(1)若m∥n,求证:△ABC为等腰三角形;
(2)若m⊥p,边长c=2,C=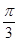 ,求△ABC的面积.
,求△ABC的面积.
已知a=(sin α,sin β),b=(cos(α-β),-1),c=(cos(α+β),2),α,β≠kπ+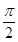 (k∈Z).
(k∈Z).
(1)若b∥c,求tan α·tan β的值;
(2)求a2+b·c的值.
△ABC中内角A,B,C的对边分别为a,b,c,已知a=bcos C+csin B.
(1)求B;
(2)若b=2,求△ABC面积的最大值.