随着航母编队的成立,我国海军日益强大.2018年4月12日,中央军委在南海海域隆重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到 处时,该舰在观测点 的南偏东 的方向上,且与观测点 的距离 为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点 的北偏东 方向上的 处,问此时巡逻舰与观测点 的距离 为多少海里?(参考数据: , ,结果精确到1海里).

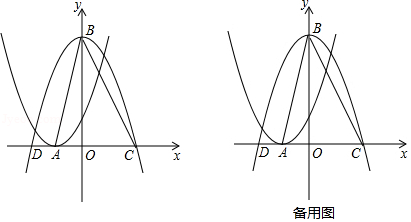
如图所示,将二次函数 的图象沿 轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数 的图象.函数 的图象的顶点为点 .函数 的图象的顶点为点 ,和 轴的交点为点 , (点 位于点 的左侧).
(1)求函数 的解析式;
(2)从点 , , 三个点中任取两个点和点 构造三角形,求构造的三角形是等腰三角形的概率;
(3)若点 是线段 上的动点,点 是 三边上的动点,是否存在以 为斜边的 ,使 的面积为 面积的 ?若存在,求 的值;若不存在,请说明理由.
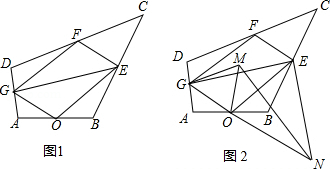
如图 1 所示, 在四边形 中, 点 , , , 分别是 , , , 的中点, 连接 , , , , .
(1) 证明: 四边形 是平行四边形;
(2) 将 绕点 顺时针旋转得到 ,如图 2 所示, 连接 , .
①若 , ,求 的值;
②试在四边形 中添加一个条件, 使 , 的长在旋转过程中始终相等 . (不 要求证明)
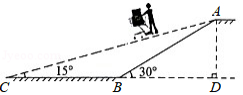
某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯 长为 ,坡角 为 ;改造后的斜坡式自动扶梯的坡角 为 ,请你计算改造后的斜坡式自动扶梯 的长度,(结果精确到0. ,温馨提示: ,
某公司计划购买 , 两种型号的机器人搬运材料.已知 型机器人比 型机器人每小时多搬运 材料,且 型机器人搬运 材料所用的时间与 型机器人搬运 材料所用的时间相同.
(1)求 , 两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购 , 两种型号的机器人共20台,要求每小时搬运材料不得少于 ,则至少购进 型机器人多少台?