在平面直角坐标系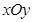 中,已知点
中,已知点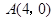 ,动点
,动点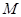 在
在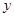 轴上的正射影为点
轴上的正射影为点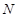 ,且满足直线
,且满足直线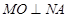 .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)当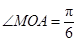 时,求直线
时,求直线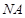 的方程.
的方程.
在△ 中,已知
中,已知 、
、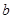 、
、 分别是三内角
分别是三内角 、
、 、
、 所对应的边长,且
所对应的边长,且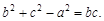
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,且△
,且△ 的面积为
的面积为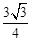 ,求
,求
已知命题 :实数m满足
:实数m满足 ,命题
,命题 :函数
:函数 是增函数。若
是增函数。若 为真命题,
为真命题, 为假命题,则实数m的取值范围为
为假命题,则实数m的取值范围为
数列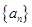 的前
的前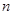 项和记为
项和记为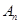 ,
, ,
,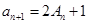 (
(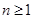 )(Ⅰ)求
)(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)等差数列 的各项为正,其前
的各项为正,其前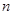 项和为
项和为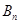 ,且
,且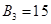 ,又
,又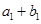 ,
,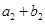 ,
,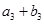 成等比数列,求
成等比数列,求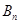 的表达式;
的表达式;
(3)若数列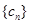 中
中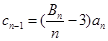 (
(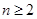 ),求数列
),求数列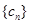 的前
的前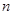 项和
项和 的
的
表达式.
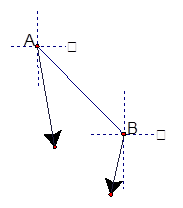
如图所示,巡逻艇在A处测得某走私船在东偏南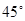 方向距A处9海里的B处,正向南偏西
方向距A处9海里的B处,正向南偏西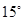 方向行驶,速度为20海里/小时,如果巡逻艇以航速28海里/小时,则应在什么方向用多少时间才能追上这艘走私艇?(
方向行驶,速度为20海里/小时,如果巡逻艇以航速28海里/小时,则应在什么方向用多少时间才能追上这艘走私艇?(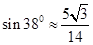 )
)
一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤.但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元.现该农民手头有400元,两种作物各种多少,才能获得最大收益?