在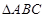 中,
中, 分别是角A,B,C的对边,且满足
分别是角A,B,C的对边,且满足 .
.
(1)求角B的大小;
(2)若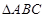 最大边的边长为
最大边的边长为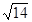 ,且
,且 ,求最小边长.
,求最小边长.
(本小题满分10分)
已知四棱锥P—ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点。
(I)求AC与PB所 成角的余弦值;
成角的余弦值;
(II)求面AMC与面BMC所成二面角的余弦值的大小。
(选修4—5:不等式选讲)
设x是正数,求证:
(选修4—4:坐标系与参数方程)
已知两个圆的极坐标方程分别是 ,求这两个圆的圆心距。
,求这两个圆的圆心距。
(选修4—2:矩阵与变换)
已知矩阵 ,矩阵M对应的变换把曲线
,矩阵M对应的变换把曲线 变为曲线C,求曲线C的方程。
变为曲线C,求曲线C的方程。
(选修4—1:几何证明选讲)
如图,AB是⊙O的直径,C、F为⊙O上的点,且CA平分∠BAF,过点C作CD⊥AF,交AF的延长线于点D。
求证:DC是⊙O的切线。