已知抛物线 的焦点F也是椭圆
的焦点F也是椭圆
 的一个焦点,
的一个焦点, 与
与 的公共弦长为
的公共弦长为 ,过点F的直线
,过点F的直线 与
与 相交于
相交于 两点,与
两点,与 相交于
相交于 两点,且
两点,且 与
与 同向.
同向.
(Ⅰ)求 的方程;
的方程;
(Ⅱ)若 ,求直线
,求直线 的斜率.
的斜率.
(满分9分)如图,已知梯形 中,
中, ,
, 。求梯形的高.
。求梯形的高.
(本题满分14分) 设函数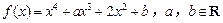 .
.
(Ⅰ)当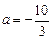 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(Ⅱ)若函数 仅在x=0处有极值,试求a的取值范围;
仅在x=0处有极值,试求a的取值范围;
(Ⅲ)若对于任何 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
(本题满分14分) 口袋中有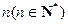 个白球和3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X.若
个白球和3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X.若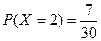 ,求:
,求:
(1)n的值;
(2)X的概率分布与数学期望.
(本题满分14分) 已知 为直线
为直线 ,
,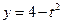 及
及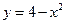 所围成的面积,
所围成的面积,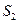 为直线
为直线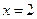 ,
,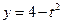 及
及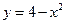 所围成图形的面积(
所围成图形的面积( 为常数).
为常数).
(1)若 时,求
时,求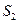 ;
;
(2)若 ,求
,求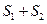 的最大值.
的最大值.
(本小题满分14分)在二项式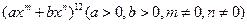 中有2m+n=0,如果它的展开式里最大系数项恰是常数项.
中有2m+n=0,如果它的展开式里最大系数项恰是常数项.
(1) 求它是第几项;(2)求
求它是第几项;(2)求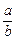 的范围.
的范围.