如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.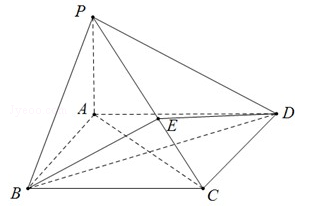
(1)证明:BD⊥平面PAC;
(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.
已知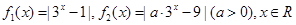 ,
,
且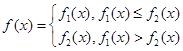 .
.
(Ⅰ)当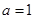 时,求
时,求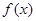 在
在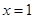 处的切线方程;
处的切线方程; (Ⅱ)当
(Ⅱ)当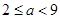 时,设
时,设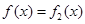 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为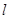 (闭区间
(闭区间 的长度定义为
的长度定义为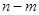 ),试求
),试求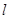 的最大值;
的最大值;
(Ⅲ)是否存在这样的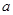 ,使得当
,使得当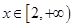 时,
时,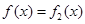 ?若存在,求出
?若存在,求出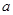 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知椭圆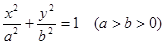 的离心率为
的离心率为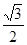 ,椭圆的左、右两个顶点分别为
,椭圆的左、右两个顶点分别为 ,
,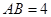 ,直线
,直线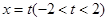 与椭圆相交于
与椭圆相交于 两点,经过三点
两点,经过三点 的圆与经过三点
的圆与经过三点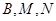 的圆分别记为圆C1与圆C2.
的圆分别记为圆C1与圆C2.
(1)求椭圆的方程;
(2)求证:无论 如何变化,圆C1与圆C2的圆心距是定值;
如何变化,圆C1与圆C2的圆心距是定值;
(3)当 变化时,求圆C1与圆C2的面积的和
变化时,求圆C1与圆C2的面积的和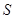 的最小值.
的最小值.
已知函数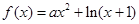
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数 在区间
在区间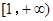 上为减函数,求实数
上为减函数,求实数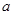 的取值范围
的取值范围
(3)当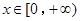 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数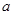 的取值范围.
的取值范围.
等比数列 满足
满足 的前n项和为
的前n项和为 ,且
,且
(1)求 ;
;
(2)数列 的前n项和,是否存在正整数m,
的前n项和,是否存在正整数m, ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可吸入肺颗粒物。我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米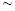 75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。某试点城市环保局从该市市区2013年上半年每天的PM2.5监测数据中随机的抽取15天的数据作为样本,监测值如图茎叶图所示(十位为茎,个位为叶)。
75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。某试点城市环保局从该市市区2013年上半年每天的PM2.5监测数据中随机的抽取15天的数据作为样本,监测值如图茎叶图所示(十位为茎,个位为叶)。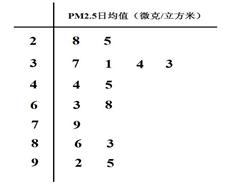
(1)求PM2.5日均值在75微克/立方米以下的平均数与中位数;
(2)从这15天的数据中任取2天数据,记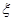 表示抽到PM2.5监测数据超标的天数,求
表示抽到PM2.5监测数据超标的天数,求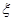 的分布列及数学期望;
的分布列及数学期望;