某商店在四个月的试销期内,只销售A、B两个品牌的电视机,共售出400台.试销结束后,只能经销其中的一个品牌,为作出决定,经销人员正在绘制两幅统计图,如图1和图2.
(1)第四个月销量占总销量的百分比是___________;
(2)B品牌电视机第三个月销量是___________台;
(3)为跟踪调查电视机的使用情况,从该商店第四个月售出的电视机中,随机抽取一台,求抽到B品牌电视机的概率;
(4)经计算,两个品牌电视机月销量的平均水平相同,补全表示B品牌电视机月销量的折线,请你结合折线的走势进行简要分析,判断该商店应经销哪个品牌的电视机.
某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人,投票结果统计如图一;其次,对三名候选人进行了笔试和面试两项测试,各项成绩如下表所示;图二是某同学根据右下表绘制的一个不完整的条形图.

请你根据以上信息解答下列问题:补全图一和图二
请计算每名候选人的得票数;
若每名候选人得一票记1分,投票、笔试、面试三项
得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
解方程: .
.
已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线
y=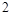 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).求抛物线的解析式
设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得
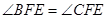 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由射线OC上有两个动点P、Q同时从原点出发,分别以每秒
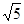 个单位长度、每秒2
个单位长度、每秒2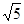 个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
在△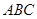 中,
中,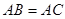 ,
,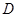 是底边
是底边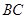 上一点,
上一点,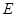 是线段
是线段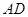 上一点,且
上一点,且
∠ .
.如图1,若∠
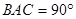 ,猜想
,猜想 与
与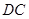 的数量关系为;
的数量关系为;如图2,若∠
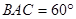 ,猜想
,猜想 与
与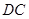 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;若∠
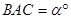 ,请直接写出
,请直接写出 与
与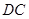 的数量关系.
的数量关系.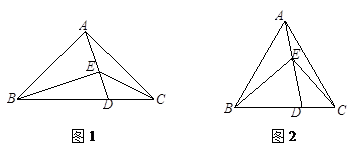
已知:直线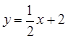 分别与 x轴、y轴交于点A、点B,点P(
分别与 x轴、y轴交于点A、点B,点P(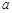 ,b)在直线AB 上,点P关于
,b)在直线AB 上,点P关于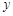 轴的对称点P′ 在反比例函数
轴的对称点P′ 在反比例函数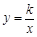 图象上.
图象上.当a=1时,求反比例函数
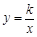 的解析式
的解析式设直线AB与线段P'O的交点为C.当P'C =2CO时,求b的值;
过点A作AD//y轴交反比例函数图象于点D,若AD=
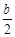 ,求△P’DO的面积.
,求△P’DO的面积. 