由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| |
支持 |
保留 |
不支持 |
| 20岁以下 |
800 |
450 |
200 |
| 20岁以上(含20岁) |
100 |
150 |
300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取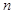 个人,已知从“支持”态度的人中抽取了45人,求
个人,已知从“支持”态度的人中抽取了45人,求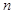 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有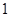 人20岁以下的概率;
人20岁以下的概率;
(本小题满分13分)如图,在矩形纸片ABCD中,AB=6,BC=12.将矩形纸片在右下角折起,使得该角的顶点落在矩形有左边上,设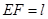 ,
,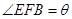 ,那么的长度取决于角
,那么的长度取决于角 的大小.
的大小.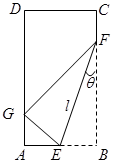
(1)写出用 表示
表示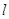 的函数关系式,并给出定义域;
的函数关系式,并给出定义域;
(2)求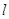 的最小值.
的最小值.
(本小题满分12分)已知正项数列 的首项
的首项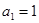 ,前
,前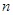 项和
项和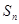 满足
满足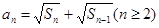 .
.
(1)求证: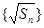 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(2)记数列 的前
的前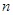 项和为
项和为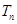 ,若对任意的
,若对任意的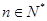 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)如图,已知四棱锥的侧棱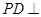 底面
底面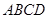 ,且底面
,且底面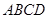 是直角梯形,
是直角梯形,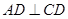 ,
, ,
,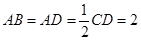 ,点
,点 在侧棱上.
在侧棱上.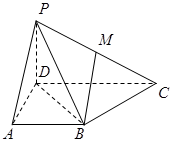
(1)求证: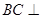 平面
平面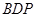 ;
;
(2)若侧棱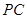 与底面
与底面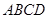 所成角的正切值为
所成角的正切值为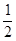 ,点
,点 为侧棱
为侧棱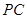 的中点,求异面直线
的中点,求异面直线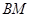 与
与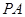 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)编号分别为A1,A2, ,A16的16名校篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
| 得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
| 运动员编号 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
| 得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(1)将得分在对应区间内的人数填入相应的空格:
| 区间 |
[10,20) |
[20,30) |
[30,40] |
| 人数 |
(2)从得分在区间[20,30)内的运动员中随机抽取2人,①用运动员编号列出所有可能的抽取结果;②求这2人得分之和大于50的概率.
设函数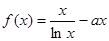 .
.
(1)若函数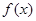 在
在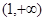 上为减函数,求实数
上为减函数,求实数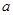 的最小值;
的最小值;
(2)若存在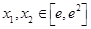 ,使
,使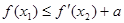 成立,求实数
成立,求实数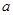 的取值范围.
的取值范围.