设集合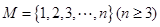 ,记
,记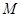 的含有三个元素的子集个数为
的含有三个元素的子集个数为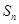 ,同时将每一个子集中的三个元素由小到大排列,取出中间的数,所有这些中间的数的和记为
,同时将每一个子集中的三个元素由小到大排列,取出中间的数,所有这些中间的数的和记为 .
.
(1)求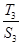 ,
, ,
, ,
,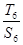 的值;
的值;
(2)猜想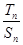 的表达式,并证明之.
的表达式,并证明之.
(本小题满分12分)已知函数 (其中
(其中 ,
,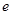 是自然对数的底数
是自然对数的底数
(1)若 ,判断函数
,判断函数 在区间
在区间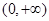 上的单调性;
上的单调性;
(2)若函数 有两个极值点
有两个极值点 ,
, ,求
,求 的取值范围;
的取值范围;
(3)在(2)的条件下,试证明: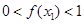 .
.
(本小题满分12分)若函数 是定义域
是定义域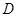 内的某个区间
内的某个区间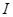 上的增函数,且
上的增函数,且 在
在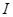 上是减函数,则称
上是减函数,则称 是I上的“非完美增函数”,已知
是I上的“非完美增函数”,已知 ,
, .
.
(1)判断 在
在 上是否是“非完美增函数”;
上是否是“非完美增函数”;
(2)若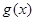 是
是 上的“非完美增函数”,求实数
上的“非完美增函数”,求实数 的取值范围.
的取值范围.
(本小题满分12分)在 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,且
,且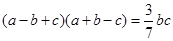 .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的面积.
的面积.
(本小题满分12分)已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)试确定函数 的解析式;
的解析式;
(2)若 ,求
,求 的值.
的值.
(本小题满分12分)已知向量 ,
, ,函数
,函数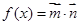 .
.
(1)求函数 的最大值,并写出相应
的最大值,并写出相应 的取值集合;
的取值集合;
(2)若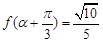 ,且
,且 ,求
,求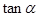 的值.
的值.