如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了t秒.
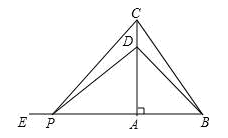
(1)求AD的长.
(2)直接写出用含有t的代数式表示PE= .
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出t值;若不存在,请说明理由.
如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
如图,平地上一幢建筑物AB与铁塔CD相距40m,在建筑物的顶部测得铁塔底部的俯角为37°,测得铁塔顶部的仰角为26.6°,求铁塔的高度.
(参考数据:sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)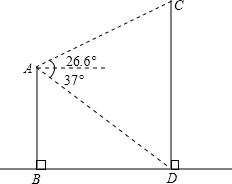
学校举行数学知识竞赛,设立了一、二、三等奖,计划共购买45件奖品,其中二等奖奖品件数比一等奖奖品件数的2倍还少5件,已知购买一等奖奖品x件.各种奖品的单价如下表:
| 奖品 |
一等奖奖品 |
二等奖奖品 |
三等奖奖品 |
| 单价(元) |
12 |
10 |
8 |
(1)学校购买二等奖奖品件,三等奖奖品件;(用含x的代数式表示)
(2)若购买三等奖奖品的费用不超过二等奖奖品的费用的2倍,学校为节省开支,应如何购买这三种奖品?总费用最少是多少元?
“低碳环保,你我同行”,两年来,南京市区的公共自行车给市民出行带来切实方便,电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多九使用一次公共自行车?”,将本次调查结果归为四种情况:A 每天都用;B 经常使用;C 偶尔使用;D 从未使用.将这次调查情况整理并绘制如下两幅统计图:
根据图中的信息,解答下列问题:
(1)本次活动共有位市民参与调查;
(2)补全条形统计图;
(3)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?
在不透明的袋子中有四张标着数字1,2,3,4 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是他所画的树状图的一部分.
(1)由如图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后(填“放回”或“不放回”),再随机抽出一张卡片;
(2)帮甲同学完成树状图;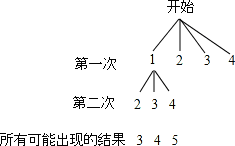
(3)求甲同学两次抽到的数字之和为偶数的概率.