如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.


(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的容积: _________ cm3.
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,已知点A(-1,1),现将A点先向左平移3个单位,再向下平移4个单位得到点B,然后作点B关于 轴的对称点得到C点,最后做点C关于
轴的对称点得到C点,最后做点C关于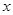 轴的对称点得到D点。
轴的对称点得到D点。
在坐标系中作出点A、B、C、D。
顺次连接ABCDA,求四边形ABCD的面积。
如图:已知AB∥DE∥CF,若∠ABC=60°,∠CDE=140°,求∠BCD的度数。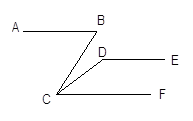
如图,在平面直角坐标系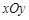 中,
中,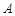 、
、 为
为 轴上两点,
轴上两点,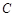 、
、 为
为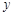 一上两点,经过点
一上两点,经过点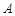 、
、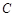 、
、 的抛物线的一部分
的抛物线的一部分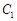 与经过点
与经过点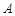 、
、
 的抛物线的一部分
的抛物线的一部分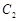 组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点
组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点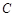 的坐标为
的坐标为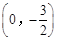 ,点
,点 是抛物线
是抛物线 的顶点.
的顶点.
(1)求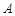 、
、 两点的坐标;
两点的坐标;
(2)“蛋线”在第四象限上是否存在一点 ,使得
,使得 的面积最大?若存在,求出
的面积最大?若存在,求出 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
(3)当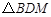 为直角三角形时,求
为直角三角形时,求 的值.
的值.
已知:四边形 中,对角线的交点为
中,对角线的交点为 ,
,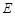 是
是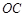 上的一点,过点
上的一点,过点 作
作 于点
于点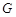 ,
, 、
、 交于点
交于点 .
.

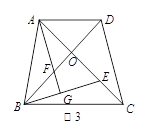
(1)如图1,若四边形 是正方形,求证:
是正方形,求证: ;
;
(2)如图2,若四边形 是菱形,
是菱形, .探究线段
.探究线段 与
与 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图3,若四边形 是等腰梯形,
是等腰梯形, ,且
,且 .结合上面的活动经验,探究线段
.结合上面的活动经验,探究线段 与
与 的数量关系为.(直接写出答案).
的数量关系为.(直接写出答案).
如图,直线与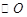 交于
交于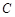 、
、 两点,且与半径
两点,且与半径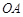 垂直,垂足为
垂直,垂足为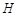 ,
,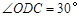 ,在
,在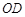 的延长线上取一点
的延长线上取一点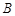 ,使得
,使得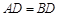 .
.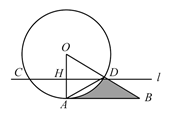
(1)判断直线 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若 的半径为2,求图中阴影部分的面积.(结果保留
的半径为2,求图中阴影部分的面积.(结果保留 )
)