篮球比赛时,运动员的进攻成功率=投球命中率×不被对方运动员的拦截率。某运动员在距球篮10米(指到篮圈圆心在地面上射影的距离)以内的投球命中率有如下变化:距球篮1米以内(不含1米)为100%.距离球篮x米处,命中率下降至 .该运动员投球被拦截率为
.该运动员投球被拦截率为 .试求该运动员在比赛时:(结果精确到
.试求该运动员在比赛时:(结果精确到 )
)
(1)在三分线(约距球篮6.72米)处的进攻成功率为多少?
(2)在距球篮几米处的进攻成功率最大,最大进攻成功率为多少?
(本小题满分12分)已知向量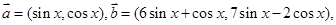
设函数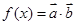
(I)求函数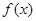 的最大值及此时x的集合;
的最大值及此时x的集合;
(Ⅱ)在A为锐角的三角形ABC中,角A、B、C的对边分别为a、b、c, 且
且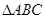
的面积为3, 求a的值。
求a的值。
(本小题满分12分)已知数列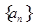 的前
的前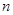 项和为
项和为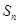 ,且
,且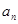 是
是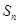 与2的等差中项,数列
与2的等差中项,数列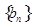 中,
中,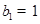 ,点
,点 在直线
在直线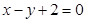 上.
上.
⑴求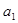 和
和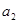 的值;
的值;
⑵求数列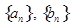 的通项
的通项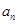 和
和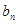 ;
;
⑶ 设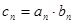 ,求数列
,求数列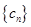 的前n项和
的前n项和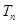 .
.
(本小题满分12分)一缉私艇发现在北偏东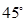 方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东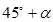 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和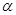 角的正弦值.
角的正弦值.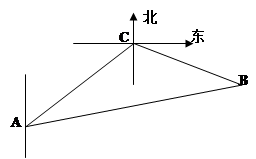
(本小题满分12分)已知二次函数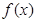 的二次项系数为
的二次项系数为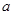 ,且不等式
,且不等式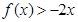 的解集为(1,3)。
的解集为(1,3)。
(1)若方程 有两个相等的实数根,求
有两个相等的实数根,求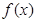 的解析式;
的解析式;
(2)若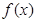 的最大值为正数,求
的最大值为正数,求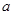 的取值范围。
的取值范围。
(本小题满分10分)已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设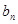 =
=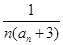 (n∈N*),
(n∈N*),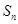 =b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有
=b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有 总成立?若存在,求出t;若不存在,请说明理由
总成立?若存在,求出t;若不存在,请说明理由