已知f(x)=x|x﹣a|+b,x∈R.
(1)当a=1,b=1时.f(2x)=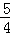 ,求x的值;
,求x的值;
(2)若b<0,b为常数,任意x∈[0,1],不等式f(x)<0恒成立,求实数a的取值范围.
已知数列
满足:
,且
.记集合
.
(Ⅰ)若
,写出集合
的所有元素;
(Ⅱ)若集合
存在一个元素是3的倍数,证明:
的所有元素都是3的倍数;
(Ⅲ)求集合
的元素个数的最大值.
已知椭圆
:
的离心率为
,点
和点
都在椭圆
上,直线
交
轴于点
.
(Ⅰ)求椭圆
的方程,并求点
的坐标(用
,
表示);
(Ⅱ)设
为原点,点
与点
关于
轴对称,直线
交
轴于点
.问:
轴上是否存在点
,使得
?若存在,求点
的坐标;若不存在,说明理由.
已知函数
.
(Ⅰ)求曲线
在点
处的切线方程;
(Ⅱ)求证:当
时,
;
(Ⅲ)设实数
使得
对
恒成立,求
的最大值.
如图,在四棱锥
中,
为等边三角形,平面
平面
,
,
,
,
,
为
的中点.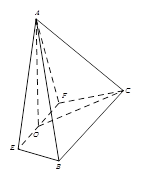
(Ⅰ)求证:
;
(Ⅱ)求二面角
的余弦值;
(Ⅲ)若
平面
,求
的值.
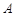 ,
, 两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下: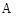 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16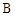 组:12,13,15,16,17,14,
组:12,13,15,16,17,14,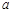
假设所有病人的康复时间互相独立,从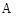 ,
,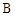 两组随机各选1人,
两组随机各选1人,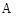 组选出的人记为甲,
组选出的人记为甲,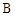 组选出的
组选出的
人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果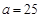 ,求甲的康复时间比乙的康复时间长的概率;
,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ)当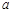 为何值时,
为何值时,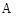 ,
,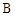 两组病人康复时间的方差相等?(结论不要求证明)
两组病人康复时间的方差相等?(结论不要求证明)