已知函数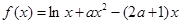 ,其中a为常数,且
,其中a为常数,且 .
.
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)在x=1处取得极值,且在(0,e]上的最大值为1,求a的值.
已知非零实数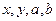 ,
,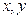 分别为
分别为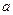 与
与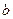 ,
,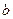 与
与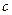 的等差中项,`且满足
的等差中项,`且满足 ,求证:非零实数
,求证:非零实数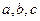 成等比数列.
成等比数列.
已知实数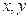 满足:
满足: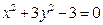 ,求
,求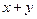 的取值范围.
的取值范围.
(本小题共13分)
用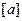 表示不大于
表示不大于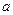 的最大整数.令集合
的最大整数.令集合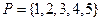 ,对任意
,对任意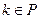 和
和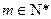 ,定义
,定义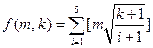 ,集合
,集合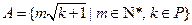 ,并将集合
,并将集合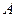 中的元素按照从小到大的顺序排列,记为数列
中的元素按照从小到大的顺序排列,记为数列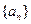 .
.
(Ⅰ)求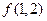 的值;
的值;
(Ⅱ)求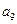 的值;
的值;
(Ⅲ)求证:在数列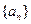 中,不大于
中,不大于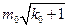 的项共有
的项共有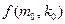 项.
项.
(本小题共14分)
已知抛物线P:x2="2py" (p>0).
(Ⅰ)若抛物线上点 到焦点F的距离为
到焦点F的距离为 .
.
(ⅰ)求抛物线 的方程;
的方程;
(ⅱ)设抛物线 的准线与y轴的交点为E,过E作抛物线
的准线与y轴的交点为E,过E作抛物线 的切线,求此切线方程;
的切线,求此切线方程;
(Ⅱ)设过焦点F的动直线l交抛物线于A,B两点,连接 ,
, 并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
(本小题共13分)
已知函数 .
.
(Ⅰ)若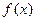 在
在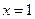 处取得极值,求a的值;
处取得极值,求a的值;
(Ⅱ)求函数 在
在 上的最大值.
上的最大值.