如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)当平面PBC与平面PDC垂直时,求PA的长.
解关于 的不等式:
的不等式: 。
。
已知圆C方程为: 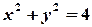
(1)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|="" ,求直线l的方程;
(2)过圆C上一动点M作平行于x轴的直线m,设m与y轴的交点为N,若向量 ,求动点Q的轨迹方程。
,求动点Q的轨迹方程。
为迎接世博会,要设计如图的一张矩形广告,该广告含有大小 相等的左中右三个矩形栏目,这三栏的面积之和为60 000
相等的左中右三个矩形栏目,这三栏的面积之和为60 000  ,四周空白的宽度为10 cm,栏与栏之间的中缝空白的宽度为5 cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.
,四周空白的宽度为10 cm,栏与栏之间的中缝空白的宽度为5 cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.
已知 当
当 时,
时, 恒成立,求a的取值范
恒成立,求a的取值范 围
围
已知等腰直角三角形ABC中,C=90°,直角边BC在直线2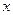 +3y-6=0上,顶点A的坐标是(5,4),求边AB和AC所在的直线方程.
+3y-6=0上,顶点A的坐标是(5,4),求边AB和AC所在的直线方程.