已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动.
(Ⅰ)求线段AB的中点轨迹方程M;
(Ⅱ)求轨迹M上的点到点P(5,4)的最小距离.
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,得曲线
轴的非负半轴为极轴建立极坐标系,得曲线 的极坐标方程为
的极坐标方程为 (
( )
)
(Ⅰ)求曲线 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线 :
:  (
(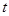 为参数)过曲线
为参数)过曲线 与
与 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线 平行且与曲线
平行且与曲线 相切的直线方程
相切的直线方程
设 (
( 且
且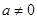 )
)
(Ⅰ)讨论函数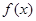 的单调性;
的单调性;
(Ⅱ)若 ,证明:
,证明: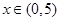 时,
时,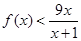 成立
成立
已知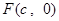 是椭圆
是椭圆 的右焦点,圆
的右焦点,圆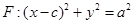 与
与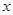 轴交于
轴交于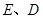 两点,
两点,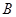 是椭圆
是椭圆 与圆
与圆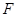 的一个交点,且
的一个交点,且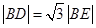
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)过点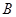 与圆
与圆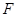 相切的直线
相切的直线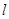 与
与 的另一交点为
的另一交点为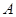 ,且
,且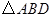 的面积为
的面积为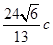 ,求椭圆
,求椭圆 的方程
的方程
如图,在直三棱柱ABC-A1B1C1中,点M是A1B的中点,点N是B1C的中点,连接MN 
(Ⅰ)证明:MN//平面ABC;
(Ⅱ)若AB=1,AC=AA1= ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小
某地区因干旱缺水,政府向市民宣传节约用水,并进行广泛动员 三个月后,统计部门在一个小区随机抽取了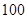 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)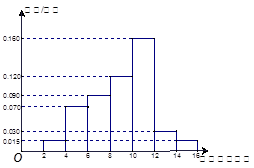

动员前动员后
(Ⅰ)已知该小区共有居民 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是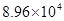 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
(Ⅱ)为了解动员前后市民的节水情况,媒体计划在上述家庭中,从政府动员前月均用水量在 范围内的家庭中选出
范围内的家庭中选出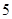 户作为采访对象,其中在
户作为采访对象,其中在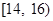 内的抽到
内的抽到 户,求
户,求 的分布列和期望
的分布列和期望