网上学习越来越受到学生的喜爱.某校信息小组为了解七年级学生网上学习的情况,从该校七年级随机抽取20名学生,进行了每周网上学习的调查.数据如下(单位:时)
3 |
2.5 |
0.6 |
1.5 |
1 |
2 |
2 |
3.3 |
2.5 |
1.8 |
2.5 |
2.2 |
3.5 |
4 |
1.5 |
2.5 |
3.1 |
2.8 |
3.3 |
2.4 |
整理上面的数据,得到表格如下:
网上学习时间(时 |
||||
人数 |
2 |
5 |
8 |
5 |
样本数据的平均数、中位数、众数如下表所示:
统计量 |
平均数 |
中位数 |
众数 |
数值 |
2.4 |
根据以上信息,解答下列问题:
(1)上表中的中位数的值为 ,众数的值为 .
(2)用样本中的平均数估计该校七年级学生平均每人一学期(按18周计算)网上学习的时间.
(3)已知该校七年级学生有200名,估计每周网上学习时间超过2小时的学生人数.
现有甲、乙、丙等多家食品公司在某市开设蛋糕店,该市蛋糕店数量的扇形统计图如图所示,其中统计图中没有标注相应公司数量的百分比.已知乙公司经营150家蛋糕店,请根据该统计图回答下列问题:
(1)求甲公司经营的蛋糕店数量和该市蛋糕店的总数.
(2)甲公司为了扩大市场占有率,决定在该市增设蛋糕店,在其余蛋糕店数量不变的情况下,若要使甲公司经营的蛋糕店数量达到全市的 ,求甲公司需要增设的蛋糕店数量.

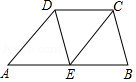
如图,在四边形 中, 是 的中点, , .
(1)求证: .
(2)当 时,求 的长.
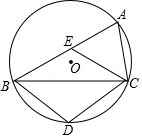
如图, 是 的内接三角形,点 在 上,点 在弦 上 不与 重合),且四边形 为菱形.
(1)求证: ;
(2)求证: ;
(3)已知 的半径为3.
①若 ,求 的长;
②当 为何值时, 的值最大?
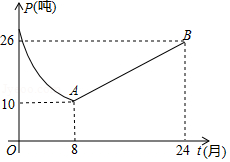
某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,并建立如下模型:设第 个月该原料药的月销售量为 (单位:吨), 与 之间存在如图所示的函数关系,其图象是函数 的图象与线段 的组合;设第 个月销售该原料药每吨的毛利润为 (单位:万元), 与 之间满足如下关系:
(1)当 时,求 关于 的函数解析式;
(2)设第 个月销售该原料药的月毛利润为 (单位:万元)
①求 关于 的函数解析式;
②该药厂销售部门分析认为, 是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量 的最小值和最大值.
如图,在 中, , ,点 , 分别在 , 上,且 .
(1)如图1,求证: ;
(2)如图2, 是 的中点,求证: ;
(3)如图3, , 分别是 , 的中点,若 , ,求 的面积.