如图,为半圆的直径,点为半圆上任一点.
(1)若,过点作半圆的切线交直线于点.求证:;
(2)若,过点作的平行线交半圆于点.当以点,,,为顶点的四边形为菱形时,求的长.

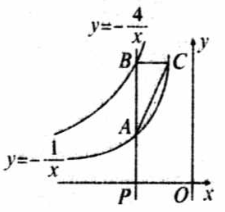
如图,点 为 轴负半轴上的一个点,过点 作 轴的垂线,交函数 的图象于点 ,交函数 的图象于点 ,过点 作 轴的平行线,交 于点 ,连接 .
(1)当点 的坐标为 时,求 的面积;
(2)若 ,求点 的坐标;
(3)连接 和 .当点 的坐标为 时, 的面积是否随 的值的变化而变化?请说明理由.
如图,在矩形 中,已知 是边 上的一个动点(不与点 重合),过 点的反比例函数 的图象与 边交于点 .
(1)求证: 与 的面积相等;
(2)记 ,求当 为何值时, 有最大值,最大值为多少?

如图,在平面直角坐标系中。已知四边形 为菱形,且 .
(1)求过点 的反比例函数解析式;
(2)设直线 与(1)中所求函数图象相切,且与 轴, 轴的交点分别为 为坐标原点.求证: 的面积为定值.

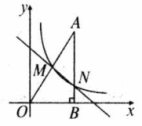
如图, 中, ,边 在 轴上,反比例函数 的图象经过斜边 的中点 ,与 相交于点N, .
(1)求 的值;
(2)求直线 的解析式.
如图所示,在平面直角坐标系 中,一次函数 的图象 与函数 的图象(记为 交于点 ,过点 作 轴于点 ,且 ,点 在线段 上(不含端点),且 ,过点 作直线 轴,交 于点 ,交图象 于点 .
(1)求 的值,并且用含 的式子表示点 的横坐标;
(2)连接 ,记 的面积分别为 ,设 ,求 的最大值.
