某中学开展主题为"垃圾分类知多少"的调查活动,调查问卷设置了"非常了解"、"比较了解"、"基本了解"、"不太了解"四个等级,要求每名学生选且只能选其中一个等级,随机抽取了120名学生的有效问卷,数据整理如下:
等级 |
非常了解 |
比较了解 |
基本了解 |
不太了解 |
人数(人 |
24 |
72 |
18 |
|
(1)求 的值;
(2)若该校有学生1800人,请根据抽样调查结果估算该校"非常了解"和"比较了解"垃圾分类知识的学生共有多少人?
对于实数a、b,定义一种新运算“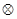 ”为:a
”为:a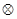 b=
b=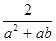 ,这里等式右边是通常的四则运算.例如:1
,这里等式右边是通常的四则运算.例如:1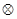 3=
3=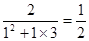 .
.
(1)解方程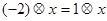 ;
;
(2)若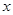 ,
,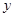 均为自然数,且满足等式
均为自然数,且满足等式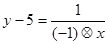 ,求满足条件的所有数对(
,求满足条件的所有数对(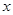 ,
,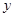 ).
).
如图,某中学操场边有一旗杆A,小明在操场的C处放风筝,风筝飞在图中的D处,在CA的延长线上离小明30米远的E处的小刚发现自己的位置与风筝D和旗杆的顶端B在同一条直线上,小刚在E处测得旗杆顶点B的仰角为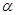 ,且tan
,且tan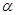 =
=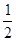 ,小明在C处测得旗杆顶点B的仰角为45°.
,小明在C处测得旗杆顶点B的仰角为45°.
(1)求旗杆的高度.
(2)此时,在C处背向旗杆,测得风筝D的仰角(即∠DCF)为48°,求风筝D离地面的距离.(结果精确到0.1米,其中sin48°≈0.74, cos48°≈0.67,tan48°≈1.11)
2014年岁末,中国多个省市出现了持续浓重的雾霾天气,截至3月底,今年主城已收获68个
蓝天,三大主要污染物PM10、二氧化硫、二氧化氮明显好转,这与各化工厂积极响应节能减排的号召分不
开.我市某化工厂从2011年就开始控制二氧化硫的排放.图1、图2分别是该厂2011-2014年二氧化硫排
放量(单位:吨)的两幅不完整的统计图,根据图中信息回答下列问题.
(1)该厂2011-2014年二氧化硫排放总量是_____吨,2011年二氧化硫的排放量对应扇形的圆心角是度,2014年二氧化硫的排放量占这四年排放总量的百分比是.并补全条形统计图.
(2)为了进一步加大环保宣传力度,重庆市环保局于年底将举行主题为“弘扬环境文化,建设绿色家园”的环保知识竞赛.该化工厂准备从刚分来的4名大学生(其中3名男生,1名女生)中选派2名员工参加比赛,请用列表法或画树状图的方法,求出所选两位参赛选手恰好是一男一女的概率.
化简:
(1)
(2)
习总书记在去年9月和10月分别提出建设“新丝绸之路经济带”和“21世纪海上丝绸之路”的战略构想,强调相关各国要打造互利共赢的“利益共同体”和共同发展繁荣的“命运共同体”.某国有企业在“一带一路” 战略合作中 ,向东南亚销售A、B两种外贸产品共6万吨.已知A种外贸产品每吨800元,B种外贸产品每吨400元.若A、B两种外贸产品销售额不低于3200万元,则至少销售A产品多少万吨?