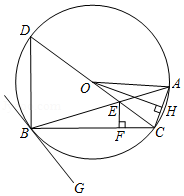
如图,内接于,是直径,,与相交于点,过点作,垂足为,过点作,垂足为,连接、.
(1)求证:直线与相切;
(2)若,求的值.
如图1,已知抛物线 与一直线相交于
与一直线相交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 ,其顶点为
,其顶点为 .
.
(1)求抛物线及直线 的函数关系式,并直接写出点
的函数关系式,并直接写出点 的坐标;
的坐标;
(2)如图1,若抛物线的对称轴与直线 相交于点
相交于点 ,
, 为直线
为直线 上的任意一点,过点
上的任意一点,过点 作
作 ∥
∥ 交抛物线于点
交抛物线于点 ,以
,以 ,
, ,
, ,
, 为顶点的四边形能否为平行四边形?若能,求点
为顶点的四边形能否为平行四边形?若能,求点 的坐标;若不能,请说明理由;
的坐标;若不能,请说明理由;
(3)如图2,若点 是抛物线上位于直线
是抛物线上位于直线 上方的一个动点,求
上方的一个动点,求 的面积的最大值.
的面积的最大值.
在边长为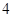 的正方形
的正方形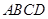 中,点
中,点 是正方形对角线的交点,动点
是正方形对角线的交点,动点 在射线
在射线 上运动,过点
上运动,过点 作线段
作线段 的垂线,交线段
的垂线,交线段 于点
于点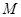 ,交直线
,交直线 于点
于点 ,连结
,连结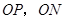 .
.
当点 在线段
在线段 上运动时,如图1所示;当点
上运动时,如图1所示;当点 在线段
在线段 的延长线上运动时,如图2所示.
的延长线上运动时,如图2所示.
(1)选择图1证明:① ;②
;②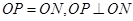 .
.
(2)设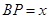 ,求以
,求以 、
、 、
、 、
、 为顶点的四边形的面积
为顶点的四边形的面积 与
与 的函数关系.
的函数关系.
在抗震救灾活动中,某厂接到一份订单,要求生产7200顶帐篷支援地震灾区,后来由于情况紧急,接收到上级指示,要求生产总量比原计划增加20%,且必须提前4天完成生产任务,该厂迅速加派人员组织生产,实际每天比原计划每天多生产720顶,请问该厂实际每天生产多少顶帐篷?
(1)如图,过反比例函数 图象上任意一点P(x,y),分别向x轴与y轴作垂线,垂线段分别为PA、PB,证明:
图象上任意一点P(x,y),分别向x轴与y轴作垂线,垂线段分别为PA、PB,证明: ,
, ,
, .
.
(2) 如图,反比例函数 的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,求k的值.
的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,求k的值.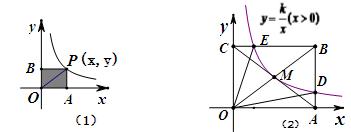
一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球.求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将 个白球放入布袋,搅匀后,使摸出1个球是白球的概率为
个白球放入布袋,搅匀后,使摸出1个球是白球的概率为 ,求
,求 的值.
的值.