如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于 ,点A坐标为 ,点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式.
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由.
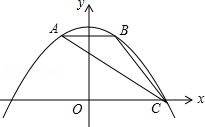
(百色)抛物线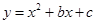 经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
(1)求抛物线与x轴的交点坐标;
(2)若点C为抛物线与x轴的交点,是否存在点D,使A、B、C、D四点围成的四边形是平行四边形?若存在,求点D的坐标;若不存在,说明理由;
(3)问几秒钟时,B、D、E在同一条直线上?
(百色)已知⊙O为△ABC的外接圆,圆心O在AB上.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.
①求证:OD⊥BC;
②求EF的长.
(百色)某次知识竞赛有20道必答题,每一题答对得10分,答错或不答都扣5分,3道抢答题,每一题抢答对得10分,抢答错扣20分,抢答不到不得分也不扣分.甲乙两队决赛,甲队必答题得了170分,乙队必答题只答错了1题.
(1)甲队必答题答对答错各多少题?
(2)抢答赛中,乙队抢答对了第1题,又抢到了第2题,但还没作答时,甲队拉拉队队员小黄说:“我们甲队输了!”,小汪说:“小黄的话不一定对!”,请你举一例说明“小黄的话”有何不对.
(玉林防城港)已知:一次函数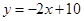 的图象与反比例函数
的图象与反比例函数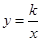 (
( )的图象相交于A,B两点(A在B的右侧).
)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若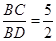 ,求△ABC的面积.
,求△ABC的面积.
(梧州)如图,抛物线 与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
(1)求此抛物线的解析式;
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标;
(3)过D点作直线DH∥AC交AB于H,当△DHF的面积最大时,在抛物线和直线AB上分别取M、N两点,并使D、H、M、N四点组成平行四边形,请你直接写出符合要求的M、N两点的横坐标.