甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）-优题课

游客

题文

甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全） $:$

运动员

环数

次数

甲

乙

$a$

$b$

某同学计算出了甲的成绩平均数是9，方差是

$S_{甲}^{2} = \frac{1}{5} [{(10 - 9)}^{2} + {(8 - 9)}^{2} + {(9 - 9)}^{2} + {(10 - 9)}^{2} + (8 - 9)^{2}] = 0.8$ ，请作答：

（1）在图中用折线统计图将甲运动员的成绩表示出来；

（2）若甲、乙射击成绩平均数都一样，则 $a + b =$ 　　；

（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出 $a$ 、 $b$ 的所有可能取值，并说明理由．

科目数学题型解答题难度中等

知识点：算术平均数方差折线统计图

登录免费查看答案和解析

相关试题

已知，直线与直线.

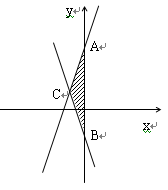
（1）求两直线与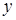轴交点A，B的坐标;
（2）求两直线交点C的坐标;
（3）求△ABC的面积.

已知直线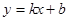经过点（1，2）和点（，4），求这条直线的解析式.

（本小题满分12分）
已知二次函数图象的顶点坐标为M(1，0)，直线与该二次函数的图象交于A，B两点，其中A点的坐标为(3，4)，B点在轴上．

（1）求m的值及这个二次函数的解析式；
（2）若P(，0) 是轴上的一个动点，过P作轴的垂线分别与直线AB和二次函数的图象交于D、E两点．
①当0<< 3时，求线段DE的最大值；
②若直线AB与抛物线的对称轴交点为N，
问是否存在一点P，使以M、N、D、E
为顶点的四边形是平行四边形？若存在，
请求出此时P点的坐标；若不存在，请
说明理由．

（本小题满分10分）
如图，AB是⊙O的直径，弦DE垂直平分半径OA，垂足为C，弦DF与半径OB相交于点P．连结EF，EO ．若DE=，∠DPA=45°

（1）求⊙O的半径；
（2）求图中阴影部分的面积．（结果保留两个有效数字）

（本小题满分10分）
设函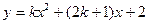数（为任意实数）
（1）求证：不论为何值，该函数图象都过点（0，2）和（－2，0）；
（2）若该函数图象与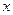轴只有一个交点，求的值．

试卷网试题网古诗词网作文网范文网