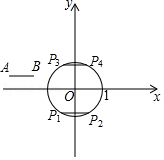
如图,在平面直角坐标系中, 的一边 在 轴上, ,点 在第一象限内, 与 轴交于点 ,抛物线 经过 、 两点,与 轴交于点 .
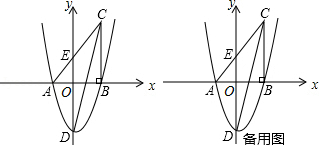
(1)请直接写出抛物线的表达式;
(2)求 的长;
(3)点 是 轴下方抛物线上一动点,设点 的横坐标为 , 的面积为 ,试求出 与 的函数关系式;
(4)若点 是 轴上一点(不与点 重合),抛物线上是否存在点 ,使 .若存在,请直接写出点 的坐标;若不存在,请说明理由.
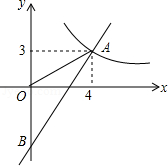
如图,一次函数 的图象分别与反比例函数 的图象在第一象限交于点 ,与 轴的负半轴交于点 ,且 .
(1)求函数 和 的表达式;
(2)已知点 ,试在该一次函数图象上确定一点 ,使得 ,求此时点 的坐标.
如图,河的两岸 与 相互平行, 、 是 上的两点, 、 是 上的两点,某人在点 处测得 , ,再沿 方向前进20米到达点 (点 在线段 上),测得 ,求 、 两点间的距离.

(1)观察下列图形与等式的关系,并填空
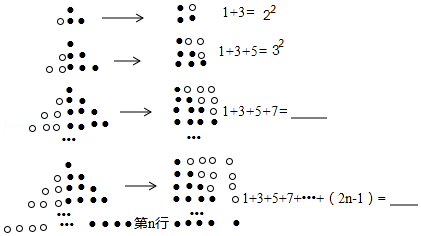
(2)观察下图,根据(1)中结论,计算图中黑球的个数,用含有
的代数式填空:
.
如图,在边长为1个单位长度的小正方形组成的 网格中,给出了四边形 的两条边 与 ,且四边形 是一个轴对称图形,其对称轴为直线 .
(1)试在图中标出点 ,并画出该四边形的另两条边;
(2)将四边形 向下平移5个单位,画出平移后得到的四边形 .
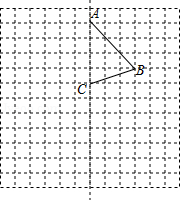
在平面直角坐标系 中, 的半径为1, , 为 外两点, .
给出如下定义:平移线段 ,得到 的弦 , 分别为点 , 的对应点),线段 长度的最小值称为线段 到 的“平移距离”.
(1)如图,平移线段 得到 的长度为1的弦 和 ,则这两条弦的位置关系是 ;在点 , , , 中,连接点 与点 的线段的长度等于线段 到 的“平移距离”;
(2)若点 , 都在直线 上,记线段 到 的“平移距离”为 ,求 的最小值;
(3)若点 的坐标为 ,记线段 到 的“平移距离”为 ,直接写出 的取值范围.