有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数 与 的图象性质.
小明根据学习函数的经验,对函数 与 ,当 时的图象性质进行了探究.
下面是小明的探究过程:
(1)如图所示,设函数 与 图象的交点为 , ,已知 点的坐标为 ,则 点的坐标为 ;
(2)若点 为第一象限内双曲线上不同于点 的任意一点.
①设直线 交 轴于点 ,直线 交 轴于点 .求证: .
证明过程如下:设 ,直线 的解析式为 .
则 ,
解得
直线 的解析式为
请你把上面的解答过程补充完整,并完成剩余的证明.
②当 点坐标为 , 时,判断 的形状,并用 表示出 的面积.

如下4个图中,不同的矩形ABCD,若把D点沿AE对折,使D点与BC上的F点重合;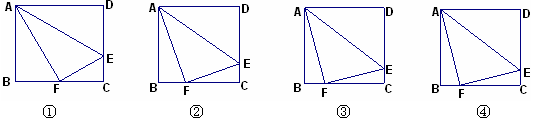
(1)图①中,若DE︰EC=2︰1,求证:△ABF∽△AFE∽△FCE;并计算BF︰FC;
(2)图②中若DE︰EC=3︰1,计算BF︰FC=;图③中若DE︰EC=4︰1,计算BF︰FC=;
(3)图④中若DE︰EC=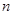 ︰1,猜想BF︰FC=;并证明你的结论
︰1,猜想BF︰FC=;并证明你的结论
如图,已知双曲线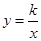 经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.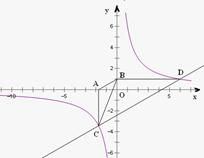
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
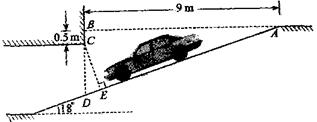
为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图。按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入。(其中AB=9m,BC=0.5m)为标明限高,请你根据该图计算CE。(精确到0.1m)(参考数值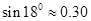 ,
,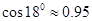 ,
,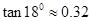 )
)
如图,梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M。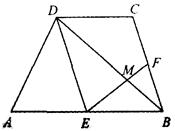
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
化简求值: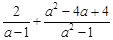 ·
·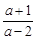 ,其中
,其中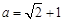 .
.