快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
解下列方程:(本题满分8分,每小题4分)
(1)4-2(3-x)=x
(2)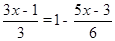
(本题12分)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm.
(1)若P、Q是△ABC边上的两个动点,其中点P从A沿A→B方向运动,速度为每秒1cm,点Q从B沿B→C方向运动,速度为每秒2cm,两点同时出发,设出发时间为t秒.
①当t=1秒时,求PQ的长;
②从出发几秒钟后,△PQB是等腰三角形?
(2)若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动,则当点M在边CA上运动时,求△BCM成为等腰三角形时M运动的时间.
(本题12分)已知实数m满足m2-3m+1=0.
(1)m+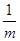 = .
= .
(2)求m2+ 的值.
的值.
(3)求m-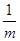 的值.
的值.
(本题12分)数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下: 

小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
(本题10分)如图,在 中,
中,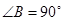 ,
, 是
是 的垂直平分线,交
的垂直平分线,交 于点
于点 ,交
,交 于点
于点 .
.
(1)若∠BAE=200,求 的度数.
的度数.
(2)若AB=6,AC=10,求BE的长.