如图（1），已知点 在正方形 的对角线 上， ，垂足为点 ， ，垂足为点 ．
（1）证明与推断：
①求证：四边形 是正方形；
②推断： 的值为
（2）探究与证明：
将正方形 绕点 顺时针方向旋转 角 ，如图（2）所示，试探究线段 与 之间的数量关系，并说明理由；
（3）拓展与运用：
正方形 在旋转过程中，当 ， ， 三点在一条直线上时，如图（3）所示，延长 交 于点 ．若 ， ，则 ．
(10分)如图：一次函数y=－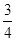
x+6的图象与x轴和y轴分别交于点A和B ,再将△AOB
沿直线CD对折，使点A与点B重合。直线CD与x轴交于点C,与AB交于点D。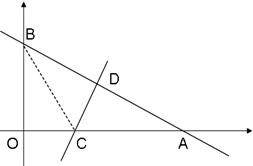
(1)点A的坐标为，点B的坐标为。
(2)求OC的长度 ；
(3)在x轴上有一点P，且△PAB是等腰三角形,不需计算过程，请直接写出点P的坐标 。
(10分) 某通讯公司推出①、②两种手机通话月收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的月通话时间x（分钟）与收费y（元）之间的函数关系如图所示．
（1）有月租费的收费方式是（填①或②），月租费是元；
（2）分别求出①，②两种收费方式中y与自变量x之间的函数关系式；
（3）请你根据用户月通话时间的多少，给出经济实惠的选择建议
(8分)如图：△ABC中，AD是高，CE是中线，G是CE的中点，DG⊥CE，G为垂足。
请说明下列结论成立的理由：
（1）DC＝BE； （2）∠B＝2∠BCE 。
如图所示，OA=OD，OB=OC，请说明下列结论成立的理由：
(1）△AOB≌△DOC； (2）AB∥CD
解不等式
，并将解集在数轴上表示出来．