【探究函数 y = x + 4 x 的图象与性质】
(1)函数 的自变量 的取值范围是 ;
(2)下列四个函数图象中函数 的图象大致是 ;

(3)对于函数 ,求当 时, 的取值范围.
请将下列的求解过程补充完整.
解:
.
拓展运用
(4)若函数 ,则 的取值范围 .
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.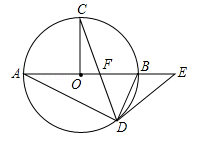
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求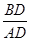 的值.
的值.
如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
如图,已知一次函数 的图象与x轴、y轴分别交于A、B两点,与反比例函数
的图象与x轴、y轴分别交于A、B两点,与反比例函数 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数 与反比例函数
与反比例函数 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出 时自变量x的取值范围.
时自变量x的取值范围.
某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价﹣进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
已知抛物线 与x轴交于点A(m-2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m-2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线y=kx+2(k≠0)与抛物线相交于两点M(x1,y1),N(x2,y2)(x1<x2),当  最小时,求抛物线与直线的交点M和N的坐标.
最小时,求抛物线与直线的交点M和N的坐标.
(3)首尾顺次连接点O,B,P,C构成多边形的周长为L.若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.