如图是小强洗漱时的侧面示意图,洗漱台(矩形 靠墙摆放,高 ,宽 ,小强身高 ,下半身 ,洗漱时下半身与地面成 ,身体前倾成 ,脚与洗漱台距离 (点 , , , 在同一直线上).
(1)此时小强头部 点与地面 相距多少?
(2)小强希望他的头部 恰好在洗漱盆 的中点 的正上方,他应向前或后退多少?
, , ,结果精确到

我国是水资源比较贫乏的国家之一,各地采用了价格调控等手段来达到节约用水的目的.某市用水收费的方法是:水费 基本费十超额费十定额损耗费.若每月用水量不超过最低限量 时,只付基本费 元和每月的定额损耗费 元;若用水量超过 时,除了付同上的基本费和定额损耗费外,超过部分每立方米付 元的超额费.已知每户每月的定额损耗费不超过 元.
(1)当月用水量为 时,支付费用为 元,写出 关于 的函数关系式;
(2)该市一家庭今年一季度的用水量和支付费用见下表,根据表中数据求 .

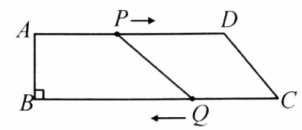
如图,在四边形 中, .点 从点 出发,以 的速度向 点运动;点 从点 同时出发,以 的速度向点 运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为 .
(1) 为何值时,四边形 是矩形?
(2) 为何值时,四边形 是平行四边形?
(3)在其它条件不变的情况下,能否通过改变点 的运动速度,使得四边形 是菱形?
设 为自然数,如果 成立,求 的值.
为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
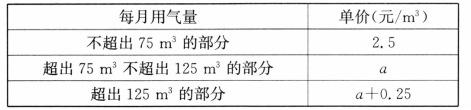
(1)若甲用户 月份的用气量为 ,则应缴费_____元;
(2)若调价后每月支出的燃气费为 (元),每月的用气量为 ( ), 与 之间的关系如下图所示,求 的值及 与 之间的函数关系式;
(3)在(2)的条件下,若乙用户 月份共用气 ( 月份用气量低于 月份用气量),共缴费 元,乙用户 月份的用气量各是多少?

某商场计划采购甲、乙、丙三种型号的“格力”牌空调共 台.三种型号的空调进价和售价如下表:

商场计划投入总资金 万元,所购进的甲、丙型号空调数量相同,乙型号数量不超过甲型号数量的一半,若设购买甲型号空调 台,所有型号空调全部售出后获得的总利润为 元.
(1)求 与 之间的函数关系式;
(2)商场如何采购空调才能获得最大利润
(3)由于原材料上涨,商场决定将丙型号空调的售价提高 元( ),其余型号售价不变,则商场又该如何采购才能获得最大利润?