如图, 的直角边 在 轴上,顶点 的坐标为 ,直线 交 于点 ,交 轴于点 .
(1)求直线 的函数表达式;
(2)动点 在 轴上从点 出发,以每秒1个单位的速度向 轴正方向运动,过点 作直线 垂直于 轴,设运动时间为 .
①点 在运动过程中,是否存在某个位置,使得 ,若存在,请求出点 的坐标;若不存在,请说明理由;
②请探索当 为何值时,在直线 上存在点 ,在直线 上存在点 ,使得以 为一边, , , , 为顶点的四边形为菱形,并求出此时 的值.

如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13, AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x
AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x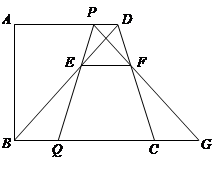
(1)求
 的值.
的值.(2)当点P运动时,试探究四边形EFGQ的面积是否会发生变化?如果发生变化,请用x的代数式表示四边形EFGQ的面积S;如果不发生变化,请求出这个四边形的面积S.
两个完全相同的矩形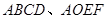 按如图所示的方式摆放,使点
按如图所示的方式摆放,使点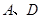 均在
均在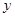 轴的正半轴上,点B在第一象限,点
轴的正半轴上,点B在第一象限,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在函数
在函数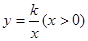 的图象上
的图象上
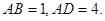

(1)求
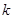 的值.
的值.(2)将矩形
 绕点B顺时针旋转
绕点B顺时针旋转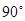 得到矩形
得到矩形 边
边 交函数
交函数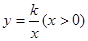 的图象于点
的图象于点 求
求 的长.
的长.
已知:如图,梯形 中,
中, 平分
平分 分别为AD、AB中点,点G为BC边上一点,且
分别为AD、AB中点,点G为BC边上一点,且
(1)求证:
 ;
;(2)猜想:当
 时,四边形
时,四边形 为平行
为平行 四边形,并说明理由.
四边形,并说明理由.
江西庐山是驰名中外的名山,为提高游客到庐山某景点的安全性,决定将到达该景点的步行台阶进行改造,把倾角由45°减至30°,已知原台 阶坡面AB的长为
阶坡面AB的长为 m(BC所在地面为水平面).
m(BC所在地面为水平面).
(1)改造后的台阶坡面会加长多少?
(2)改造后的台阶比原来的台阶多占多长一段水平地面?
如图,在△ 中,∠A=45°,
中,∠A=45°, ,
, cm,求AB的长度.
cm,求AB的长度.