问题提出
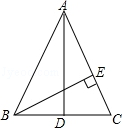
(1)如图1,在 中, , , 的平分线交 于点 .过点 分别作 , .垂足分别为 , ,则图1中与线段 相等的线段是 .
问题探究
(2)如图2, 是半圆 的直径, . 是 上一点,且 ,连接 , . 的平分线交 于点 ,过点 分别作 , ,垂足分别为 , ,求线段 的长.
问题解决
(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知 的直径 ,点 在 上,且 . 为 上一点,连接 并延长,交 于点 .连接 , .过点 分别作 , ,垂足分别为 , .按设计要求,四边形 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设 的长为 ,阴影部分的面积为 .
①求 与 之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当 的长度为 时,整体布局比较合理.试求当 时.室内活动区(四边形 的面积.

如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.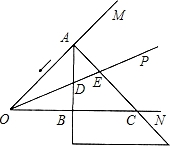
(1)点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.
(2)点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,猜想线段DF和AE有怎样的关系,并说明理由.
(3)若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,只写出结果即可.不用证明.
我们引入定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=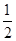 AB,求∠APB的度数.
AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.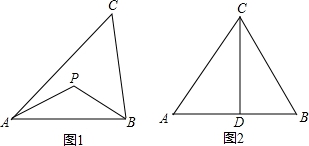
由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB = 1米,BC = 5米,两棵树的株距(两棵树的水平距离)为3米,在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?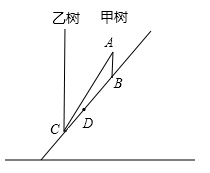
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BD=CE,BE=CF.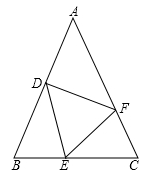
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.