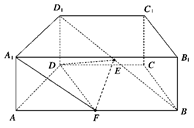
如图,在以 , , , , , 为顶点的五面体中,面 为正方形, , ,且二面角 与二面角 都是 .
(Ⅰ)证明平面 平面 ;
(Ⅱ)求二面角 的余弦值.

(本小题满分12分)
在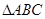 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、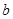 、
、 ,且满足
,且满足 .
.
(1)求角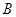 的大小;
的大小;
(2)当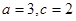 时,求
时,求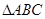 的面积.
的面积.
( (本小题满分12分)已知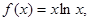
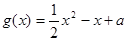 .
.
(1)当 时,求
时,求 上的值域;
上的值域;
(2) 求函数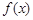 在
在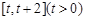 上的最小值;
上的最小值;
(3) 证明: 对一切 ,都有
,都有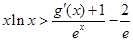 成立
成立
((本小题满分12分)
已知曲线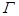 上任意一点
上任意一点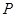 到两个定点
到两个定点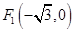 和
和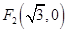 的距离之和为4.
的距离之和为4.
(1)求曲线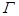 的方程;
的方程;
(2)设过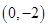 的直线
的直线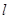 与曲线
与曲线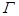 交于
交于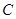 、
、 两点,且
两点,且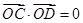 (
(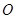 为坐标原点),求直线
为坐标原点),求直线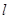 的方程.
的方程.
(.(12分)设椭圆 :
: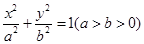 的左、右焦点分别是
的左、右焦点分别是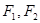 ,下顶点为
,下顶点为 ,线段
,线段 的中点为
的中点为 (
( 为坐标原点
为坐标原点 ),如图.若抛物线
),如图.若抛物线 :
: 与
与 轴的交点为
轴的交点为 ,且经过
,且经过 点.
点.
(1)求椭圆 的方程;
的方程;
(2)设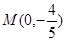 ,
,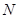 为抛物线
为抛物线 上的一动点,过点
上的一动点,过点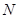 作抛
作抛 物线
物线 的切线交椭圆
的切线交椭圆 于
于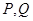 两点,求
两点,求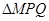 面积的最大值.
面积的最大值.
( (12分)直四棱柱 中,底面
中,底面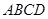 是等腰梯形,
是等腰梯形,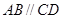 ,
,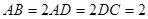 ,
, 为
为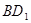 的中点,
的中点, 为
为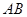 中点.
中点.
(1) 求证: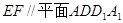 ;
;
(2) 若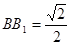 ,求
,求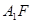 与平面
与平面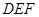 所成角的大小.
所成角的大小.