如图，⊙O的半径为6，将该圆周12等分后得到表盘模型，其中整-优题课

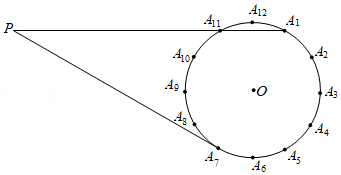
如图， $⊙ O$ 的半径为6，将该圆周12等分后得到表盘模型，其中整钟点为 $A_{n} (n$ 为 $1 ~ 12$ 的整数），过点 $A_{7}$ 作 $⊙ O$ 的切线交 $A_{1} A_{11}$ 延长线于点 $P$ ．

（1）通过计算比较直径和劣弧 $\hat{A_{7} A_{11}}$ 长度哪个更长；

（2）连接 $A_{7} A_{11}$ ，则 $A_{7} A_{11}$ 和 $P A_{1}$ 有什么特殊位置关系？请简要说明理由；

（3）求切线长 $P A_{7}$ 的值．

科目数学题型解答题难度较难

知识点：切线的判定与性质切线长定理弧长的计算

如图所示，在平面直角坐标系 $Oxy$ 中，等腰 $ΔOAB$ 的边 $OB$ 与反比例函数 $y = \frac{m}{x} (m > 0)$ 的图象相交于点 $C$ ，其中 $OB = AB$ ，点 $A$ 在 $x$ 轴的正半轴上，点 $B$ 的坐标为 $(2, 4)$ ，过点 $C$ 作 $CH ⊥ x$ 轴于点 $H$ ．

（1）已知一次函数的图象过点 $O$ ， $B$ ，求该一次函数的表达式；

（2）若点 $P$ 是线段 $AB$ 上的一点，满足 $OC = \sqrt{3} AP$ ，过点 $P$ 作 $PQ ⊥ x$ 轴于点 $Q$ ，连结 $OP$ ，记 $ΔOPQ$ 的面积为 $S_{ΔOPQ}$ ，设 $AQ = t$ ， $T = O H^{2} - S_{ΔOPQ}$

①用 $t$ 表示 $T$ （不需要写出 $t$ 的取值范围）；

②当 $T$ 取最小值时，求 $m$ 的值．

如图所示，已知正方形 $OEFG$ 的顶点 $O$ 为正方形 $ABCD$ 对角线 $AC$ 、 $BD$ 的交点，连接 $CE$ 、 $DG$ ．

（1）求证： $ΔDOG ≅ ΔCOE$ ；

（2）若 $DG ⊥ BD$ ，正方形 $ABCD$ 的边长为2，线段 $AD$ 与线段 $OG$ 相交于点 $M$ ， $AM = \frac{1}{2}$ ，求正方形 $OEFG$ 的边长．

某甜品店计划订购一种鲜奶，根据以往的销售经验，当天的需求量与当天的最高气温 $T$ 有关，现将去年六月份（按30天计算）的有关情况统计如下：

（最高气温与需求量统计表）

最高气温 $T$ （单位： $^{°} C)$	需求量（单位：杯）
$T < 25$	200
$25 ⩽ T < 30$	250
$T ⩾ 30$	400

（1）求去年六月份最高气温不低于 $30^{°} C$ 的天数；

（2）若以最高气温位于各区间的频率估计最高气温位于该区间的概率，求去年六月份这种鲜奶一天的需求量不超过200杯的概率；

（3）若今年六月份每天的进货量均为350杯，每杯的进价为4元，售价为8元，未售出的这种鲜奶厂家以1元的价格收回销毁，假设今年与去年的情况大致一样，若今年六月份某天的最高气温 $T$ 满足 $25 ⩽ T < 30$ （单位： $^{°} C)$ ，试估计这一天销售这种鲜奶所获得的利润为多少元？

小强的爸爸准备驾车外出．启动汽车时，车载报警系统显示正前方有障碍物，此时在眼睛点 $A$ 处测得汽车前端 $F$ 的俯角为 $α$ ，且 $\tan α = \frac{1}{3}$ ，若直线 $AF$ 与地面 $l_{1}$ 相交于点 $B$ ，点 $A$ 到地面 $l_{1}$ 的垂线段 $AC$ 的长度为1.6米，假设眼睛 $A$ 处的水平线 $l_{2}$ 与地面 $l_{1}$ 平行．

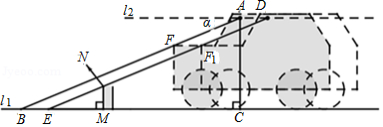
（1）求 $BC$ 的长度；

（2）假如障碍物上的点 $M$ 正好位于线段 $BC$ 的中点位置（障碍物的横截面为长方形，且线段 $MN$ 为此长方形前端的边）， $MN ⊥ l_{1}$ ，若小强的爸爸将汽车沿直线 $l_{1}$ 后退0.6米，通过汽车的前端 $F_{1}$ 点恰好看见障碍物的顶部 $N$ 点（点 $D$ 为点 $A$ 的对应点，点 $F_{1}$ 为点 $F$ 的对应点），求障碍物的高度．

先化简，再求值： $\frac{a^{2} - a}{{(a - 1)}^{2}} - \frac{a + 1}{a}$ ，其中 $a = \frac{1}{2}$ ．