已知关于 的一元二次方程 .
(1)若方程有两个不相等的实数根,求 的取值范围;
(2)二次函数 的部分图象如图所示,求一元二次方程 的解.

如图,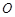 为正方形
为正方形 对角线AC上一点,以
对角线AC上一点,以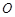 为圆心,
为圆心,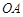 长为半径的⊙
长为半径的⊙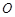 与
与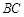 相切于点
相切于点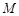 .
.
求证:
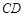 与⊙
与⊙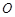 相切;
相切;若⊙
 的半径为1,求正方形
的半径为1,求正方形 的边长.
的边长.
列方程解应用题:
随着人们节能意识的增强,节能产品的销售量逐年增加.某地区高效节能灯的年销售量2009年为10万只,预计2011年将达到14.4万只.求该地区2009年到2011年高效节能灯年销售量的平均增长率.
如图,正方形 中,点F在边BC上,E在边BA的延长线上.
中,点F在边BC上,E在边BA的延长线上.若
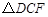 按顺时针方向旋转后恰好与
按顺时针方向旋转后恰好与 重合.则旋转中心是点;
重合.则旋转中心是点;
最少旋转了度;在(1)的条件下,若
 ,求四边形
,求四边形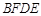 的面积.
的面积. 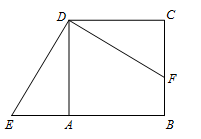
如图,在 中,AB是
中,AB是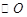 的直径,
的直径,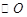 与AC交于点D,
与AC交于点D, ,
,
求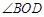 的度数;
的度数;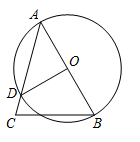
某射击运动员在相同条件下的射击160次,其成绩记录如下:
根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),
并简述理由.