某工厂有甲、乙两个车间,甲车间生产 产品,乙车间生产 产品,去年两个车间生产产品的数量相同且全部售出.已知 产品的销售单价比 产品的销售单价高100元,1件 产品与1件 产品售价和为500元.
(1) 、 两种产品的销售单价分别是多少元?
(2)随着 时代的到来,工业互联网进入了快速发展时期.今年,该工厂计划依托工业互联网将乙车间改造为专供用户定制 产品的生产车间.预计 产品在售价不变的情况下产量将在去年的基础上增加 ; 产品产量将在去年的基础上减少 ,但 产品的销售单价将提高 .则今年 、 两种产品全部售出后总销售额将在去年的基础上增加 .求 的值.
已知 ,求代数式 的值.
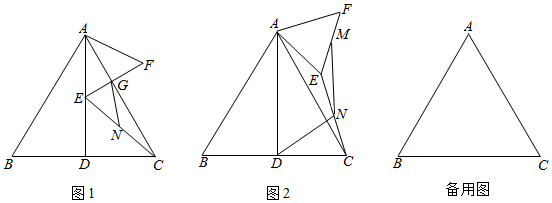
△ABC为等边三角形, , 于点D,E为线段 上一点, .以AE为边在直线 右侧构造等边三角形 ,连接 ,N为 的中点.
(1)如图1, 交于点G,连接 ,求线段 的长;
(2)如图2,将 绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接 , .当 时,猜想∠DNM的大小是否为定值,并证明你的结论;
(3)连接BN,在 绕点A逆时针旋转过程中,当线段BN最大时,请直接写出 的面积.
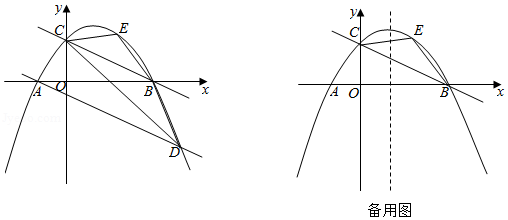
如图,在平面直角坐标系中,抛物线 与 轴交于点 ,与x轴交于 两点(点 在点 的左侧),且 点坐标为 ,直线 的解析式为 .
(1)求抛物线的解析式;
(2)过点 作 ,交抛物线于点D,点E为直线 上方抛物线上一动点,连接CE,EB,BD,DC.求四边形BECD面积的最大值及相应点E的坐标;
(3)将抛物线 向左平移 个单位,已知点 为抛物线 的对称轴上一动点,点N为平移后的抛物线上一动点.在(2)中,当四边形 的面积最大时,是否存在以 为顶点的四边形为平行四边形?若存在,直接写出点N的坐标;若不存在,请说明理由.
为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对 , 两个玉米品种进行实验种植对比研究.去年 、 两个品种各种植了10亩.收获后 、 两个品种的售价均为 元/kg,且 品种的平均亩产量比A品种高100千克, 、 两个品种全部售出后总收入为 元.
(1)求 、 两个品种去年平均亩产量分别是多少千克?
(2)今年,科技小组优化了玉米的种植方法,在保持去年种植面积不变的情况下,预计A、B两个品种平均亩产量将在去年的基础上分别增加 和 .由于B品种深受市场欢迎,预计每千克售价将在去年的基础上上涨 ,而A品种的售价保持不变, 、 两个品种全部售出后总收入将增加 .求a的值.
探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数 的图象并探究该函数的性质.
|
x |
… |
﹣4 |
﹣3 |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
4 |
… |
|
y |
… |
|
a |
﹣2 |
﹣4 |
b |
﹣4 |
﹣2 |
|
|
… |
(1)列表,写出表中 , 的值: , ;
描点、连线,在所给的平面直角坐标系中画出该函数的图象.
(2)观察函数图象,判断下列关于函数性质的结论是否正确(在答题卡相应位置正确的用“√”作答,错误的用“×”作答):
①函数 的图象关于y轴对称;
②当 时,函数 有最小值,最小值为 ;
③在自变量的取值范围内函数y的值随自变量x的增大而减小.
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.
