已知函数 .
(Ⅰ)求曲线 的斜率等于 的切线方程;
(Ⅱ)设曲线 在点 处的切线与坐标轴围成的三角形的面积为 ,求 的最小值.
设数列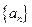 的前
的前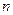 项和为
项和为 。
。
(1)证明: 为等比数列;
为等比数列;
(2)证明:求数列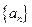 的通项公式;
的通项公式;
(3)确定 与
与 的大小关系,并加以证明。
的大小关系,并加以证明。
如图,沿等腰直角三角形 的中位线
的中位线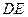 ,将平面
,将平面 折起,使得平面
折起,使得平面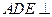 平面
平面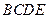 得到四棱锥
得到四棱锥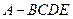 .
.
(1)求证:平面 平面
平面 ;
;
(2)过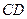 的中点
的中点 的平面
的平面 与平面
与平面 平行,试求平面
平行,试求平面 与四棱锥
与四棱锥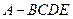 各个面的交线所围成多边形的面积与三角形
各个面的交线所围成多边形的面积与三角形 的面积之比。
的面积之比。
(3)求二面角 的余弦值。
的余弦值。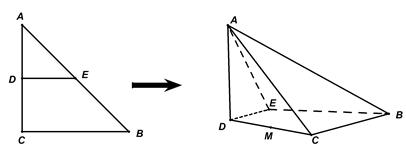
已知函数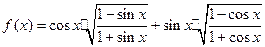
(1)求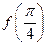 的值;
的值;
(2)写出函数函数在 上的单调区间和值域。
上的单调区间和值域。
设 , 是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离 为
对于平面 上给定的不同的两点 , ,
(Ⅰ)若点 是平面 上的点,试证明 ;
(Ⅱ)在平面 上是否存在点 ,同时满足① ;② .若存在,请求出所有符合条件的点;若不存在,请予以证明.
一条双曲线
的左、右顶点分别为
,点
是双曲线上不同的两个动点.
(1)求直线
与
交点的轨迹
的方程式;
(2)若过点
的两条直线
和
与轨迹
都只有一个交点,且
,求
的值.