已知点 A(−2,0), B(2,0),动点 M( x, y)满足直线 AM与 BM的斜率之积为− .记 M的轨迹为曲线 C.
(1)求 C的方程,并说明 C是什么曲线;
(2)过坐标原点的直线交 C于 P, Q两点,点 P在第一象限, PE⊥ x轴,垂足为 E,连结 QE并延长交 C于点 G.
(i)证明: 是直角三角形;
(ii)求 面积的最大值.
(本小题满分10分) ,
,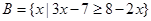
求 ,
, ,(
,(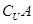 )
)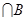
(本小题满分10分)解下列的方程、方程组及不等式组:
(1) ;
;
(2)
(本小题14分)已知直线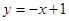 与椭圆
与椭圆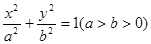 相交于A、B两点,
相交于A、B两点,
且线段AB的中点在直线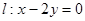 上.
上.
(1)求此椭圆的离心率;
(2)若椭圆的右焦点关于直线 的对称点的在圆
的对称点的在圆 上,求此椭圆的方程.
上,求此椭圆的方程.
(本小题满分13分)
如图,在四棱锥 中,底面
中,底面 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
,  ,
, 为
为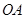 的中点,
的中点, 为
为 的中点
的中点
(Ⅰ)证明:直线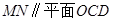
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
(本小题满分12分)
命题p:实数x满足x2-4ax+3a2<0,其中a<0,命题q:实数x满足x2-x-6≤0,且q是p的必要不充分条件,求a的取值范围.