A、B、C三个班共有 100 名学生, 为调查他们的体育锻炼情况,通过分层抽样获得了部分学生 一周的锻炼时间, 数据如下表(单位:小时);
A 班 |
|
7 |
|
|||||
B 班 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
C 班 |
3 |
|
6 |
|
9 |
|
12 |
|
(1)试估计 C 班的学生人数;
(2) 从 A 班和 班抽出的学生中, 各随机选取一人, 班选出的人记为甲, 班选出的人记 为乙, 假设所有学生的锻炼时间相对独立, 求该周甲的锻炼时间比乙的钗炼时间长的概率;
(3) 再从 A、B、C三个班中各随机抽取一名学生, 他们该周的锻炼时间分别是 7, 9, 8.25 (单位:小时), 这3个新数据与表格中的数据构成的新样本的平均数记 , 表格中数据的平均数记为 , 试判断 和 的大小, (结论不要求证明)
已知圆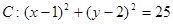 ,直线
,直线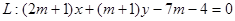
(1)求证:直线恒过定点
(2)判断直线被圆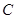 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时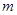 的值及最短长度。
的值及最短长度。
已知集合A= ,B=
,B=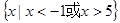 .
.
(1) 若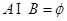 ,求实数
,求实数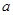 的取值范围;
的取值范围;
(2) 若 ,求实数
,求实数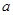 的取值范围.
的取值范围.
定义在 上的奇函数
上的奇函数 ,当
,当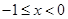 时,
时,
(1)求 在
在 上的解析式;
上的解析式;
(2)判断 在
在 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当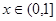 时,关于
时,关于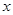 的方程
的方程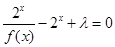 有解,试求实数
有解,试求实数 的取值范围.
的取值范围.
(本小题满分12)
为了绿化城市,准备在如图所示的区域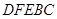 内修建一个矩形
内修建一个矩形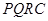 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且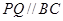 ,
,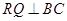 ,另外
,另外 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量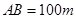 ,
,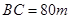 ,
, 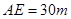 ,
,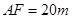 .
.
(1)求直线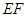 的方程;
的方程;
(2)应如何设计才能使草坪的占地面积最大?并求最大面积。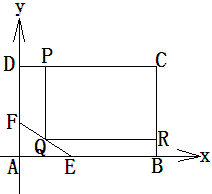
写出下列命题的否定.
(1) 对所有的正数x, 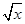 >x-1
>x-1
(2) 不存在实数x,x2+1<2x”
(3) 集合A中的任意一个元素都是集合B的元素
(4) 集合A中至少有一个元素是集合B的元素