在极坐标系中,O为极点,点 在曲线 上,直线l过点 且与 垂直,垂足为P.
(1)当 时,求 及l的极坐标方程;
(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.
如图,在直三棱柱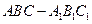 中,
中, ,
,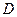 ,
, 分别为
分别为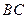 ,
, 的中点,四边形
的中点,四边形 是边长为
是边长为 的正方形.
的正方形.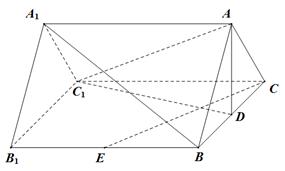
(Ⅰ)求证: ∥平面
∥平面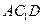 ;
;
(Ⅱ)求证: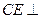 平面
平面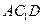 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
已知等差数列 满足:
满足: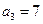 ,
, ,
, 的前n项和为
的前n项和为 .
.
(Ⅰ)求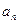 及
及 ;
;
(Ⅱ)令bn= (
( ),求数列
),求数列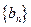 的前n项和
的前n项和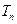 .
.
已知函数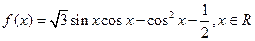 .
.
(Ⅰ) 求函数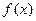 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)已知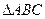 内角
内角 的对边分别为
的对边分别为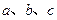 ,且
,且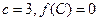 ,若向量
,若向量 与
与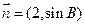 共线,求
共线,求 的值.
的值.
已知椭圆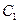 、抛物线
、抛物线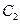 的焦点均在
的焦点均在 轴上,
轴上,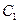 的中心和
的中心和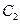 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 |
3 |
 2 2 |
4 |
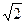 |
 |
 |
0 |
 4 4 |
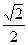 |
(Ⅰ)求 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线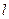 满足条件:①过
满足条件:①过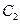 的焦点
的焦点 ;②与
;②与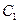 交不同两点
交不同两点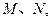 且满足
且满足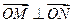 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从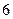 道备选题中一次性抽取
道备选题中一次性抽取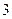 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余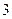 题,每人答对其中
题,每人答对其中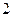 题就停止答题,即闯关成功.已知在
题就停止答题,即闯关成功.已知在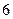 道备选题中,甲能答对其中的
道备选题中,甲能答对其中的 道题,乙答对每道题的概率都是
道题,乙答对每道题的概率都是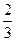 .
.
(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为ξ,求ξ的分布列及数学期望.